Regresija

Dr Nikola Grubor

2024-11-11

Vrste povezanosti

Metematički model

\(y = \alpha + \beta x\)

\(y = \text{komplikovano...}\)

Anatomija regresione jednačine (1)

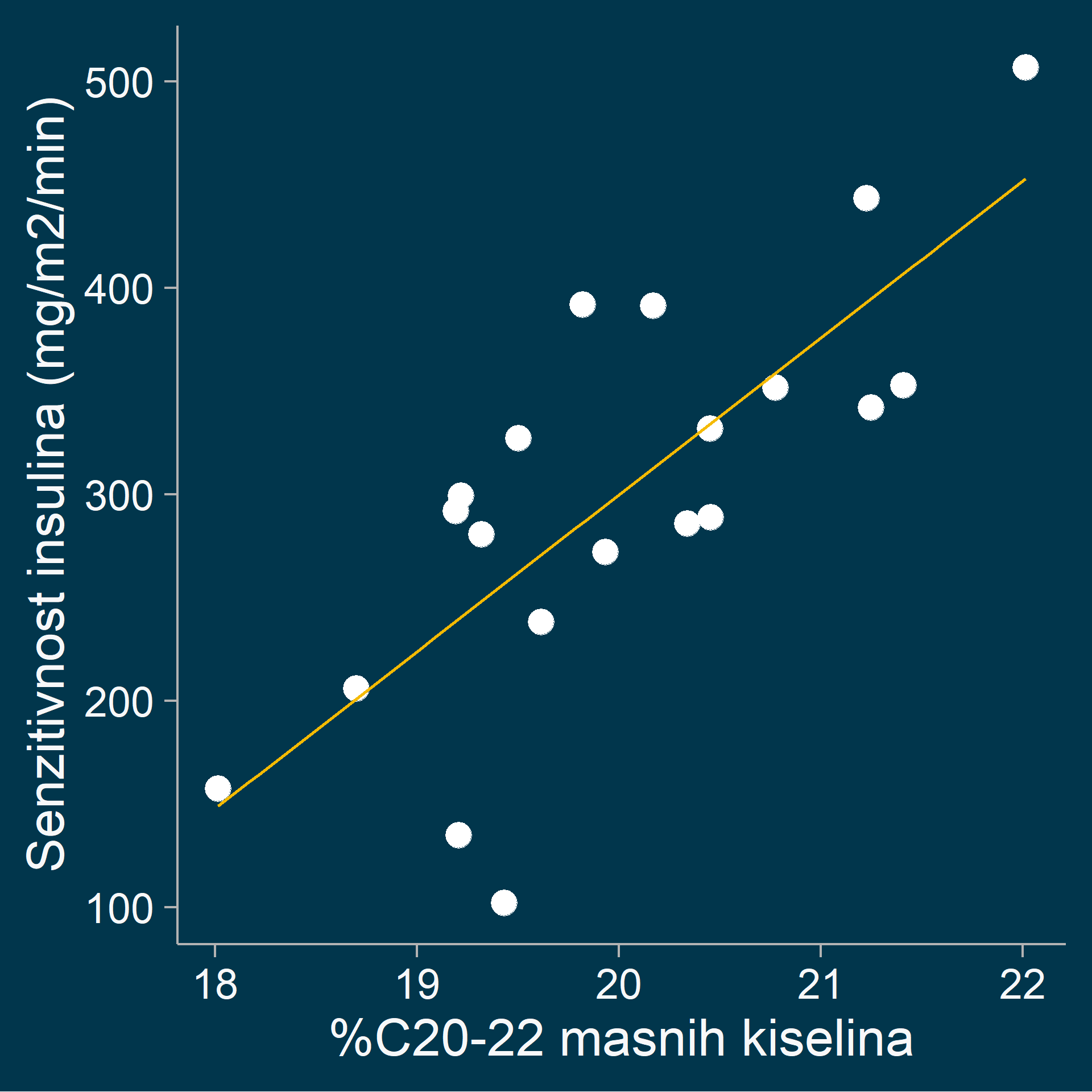
\[ y = \alpha + \beta x \]

Linearni odnos:

• \(y\), zavisna varijabla
• \(x\), nezavisna varijabla
• \(\alpha\), regresiona konstanta kad je \(x = 0\)
• \(\beta\), regresioni koeficijent (promena \(y\) ako \(x+1\))

Anatomija regresione jednačine (2)

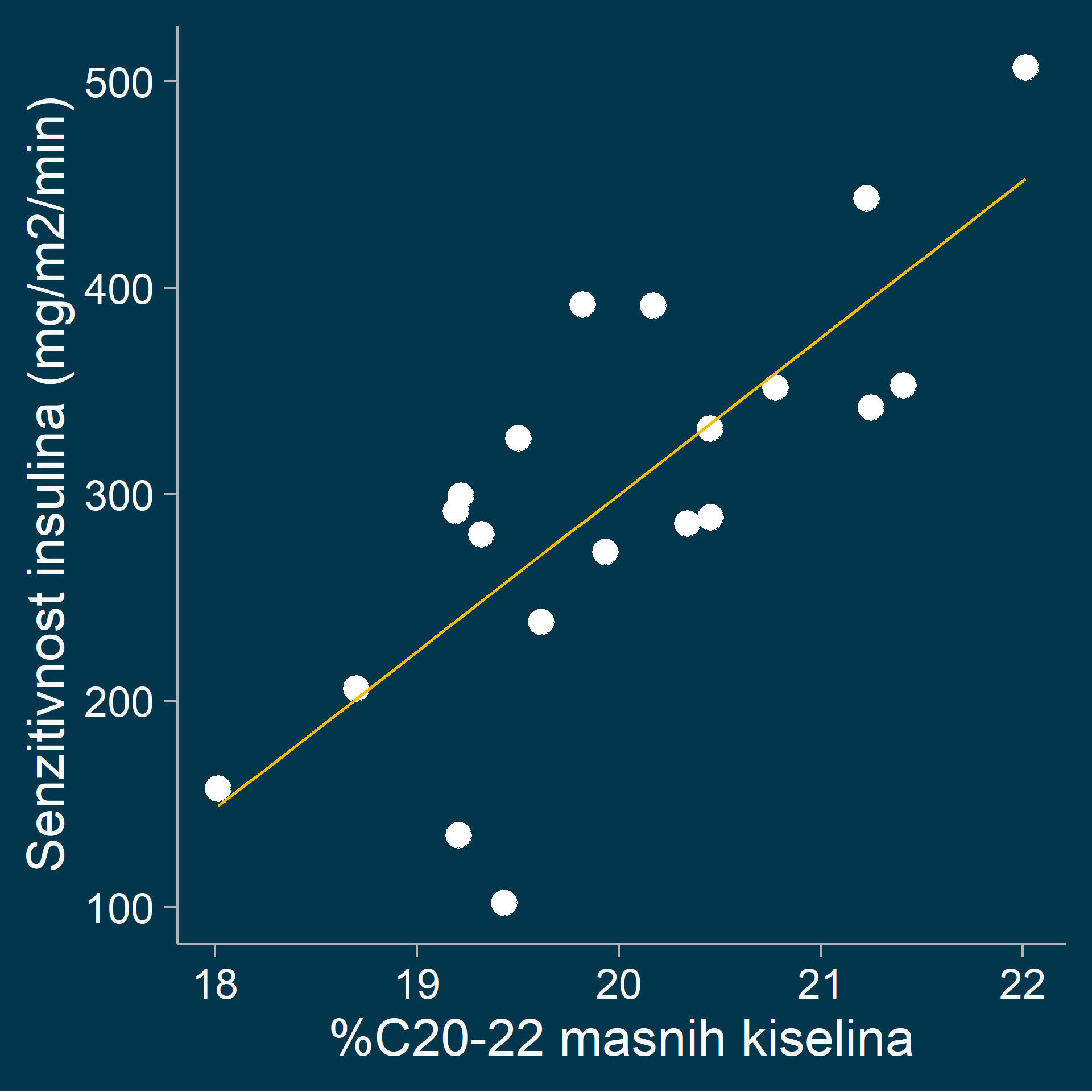
\[ y = \alpha + \beta x \]

• $ r^2 = cor(x,y)^2 $, koeficijent derterminacije (0-1, udeo objašnjene varijacije)
• $ r^2 = 0.50 $
• $ r^2 = 50 % $

Anatomija regresione jednačine (3)

term	estimate	std.error	statistic	p.value
(Intercept)	-1220	306.74	-3.98	<0.001
c20	76	15.32	4.96	<0.001

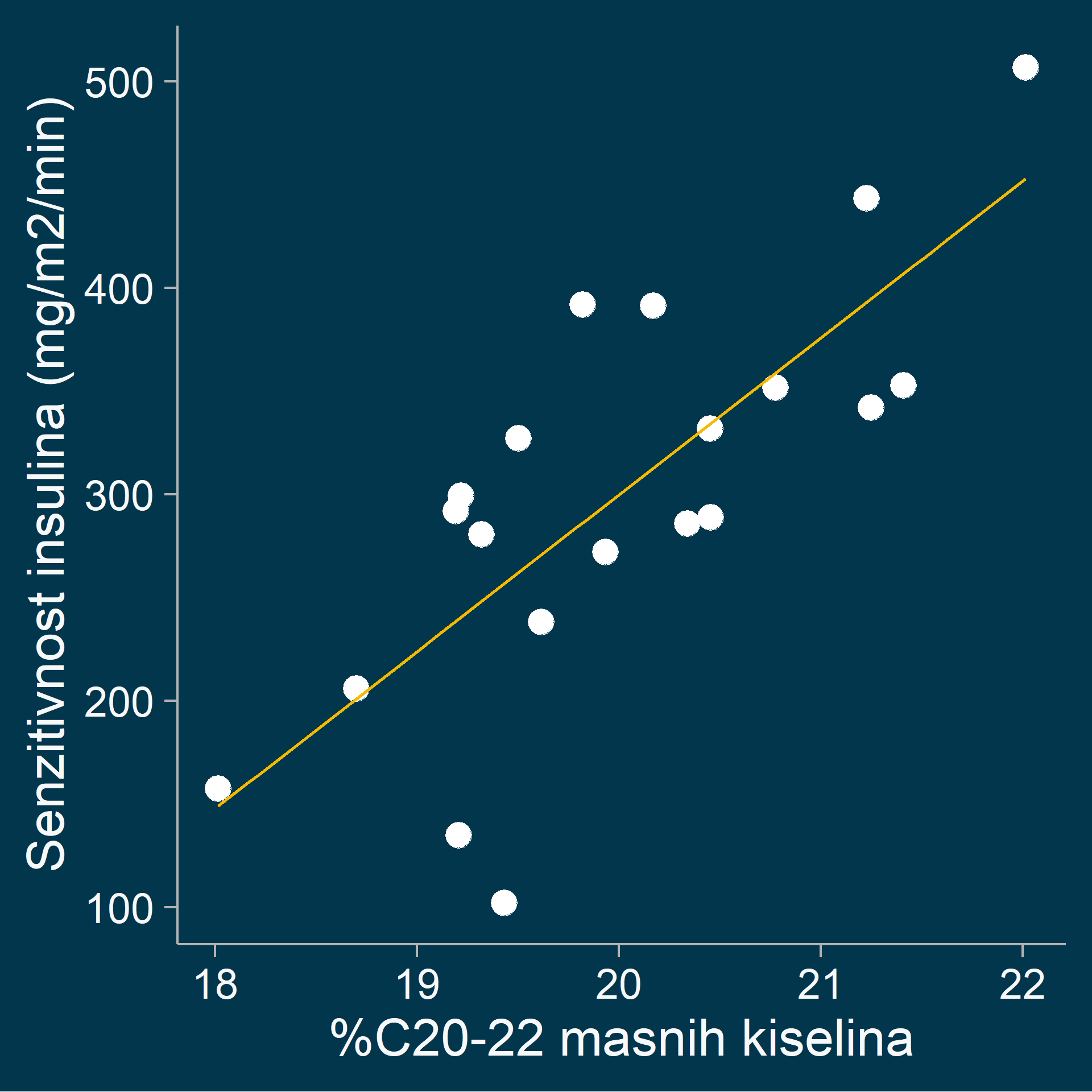
\[ y = \alpha + \beta x \]

\[ \text{insulin} = -1220 + 76 \times \text{%C20-22} \]

$ R^2 = $ 0.5776

Pretpostavke linearne regresije

1. Normalnost (reziduala*)
2. Linearnost
3. Nezavisnost (merenja nisu ponovljena)
4. Jednakost varijansi

Gde su pretpostavke ispunjene?

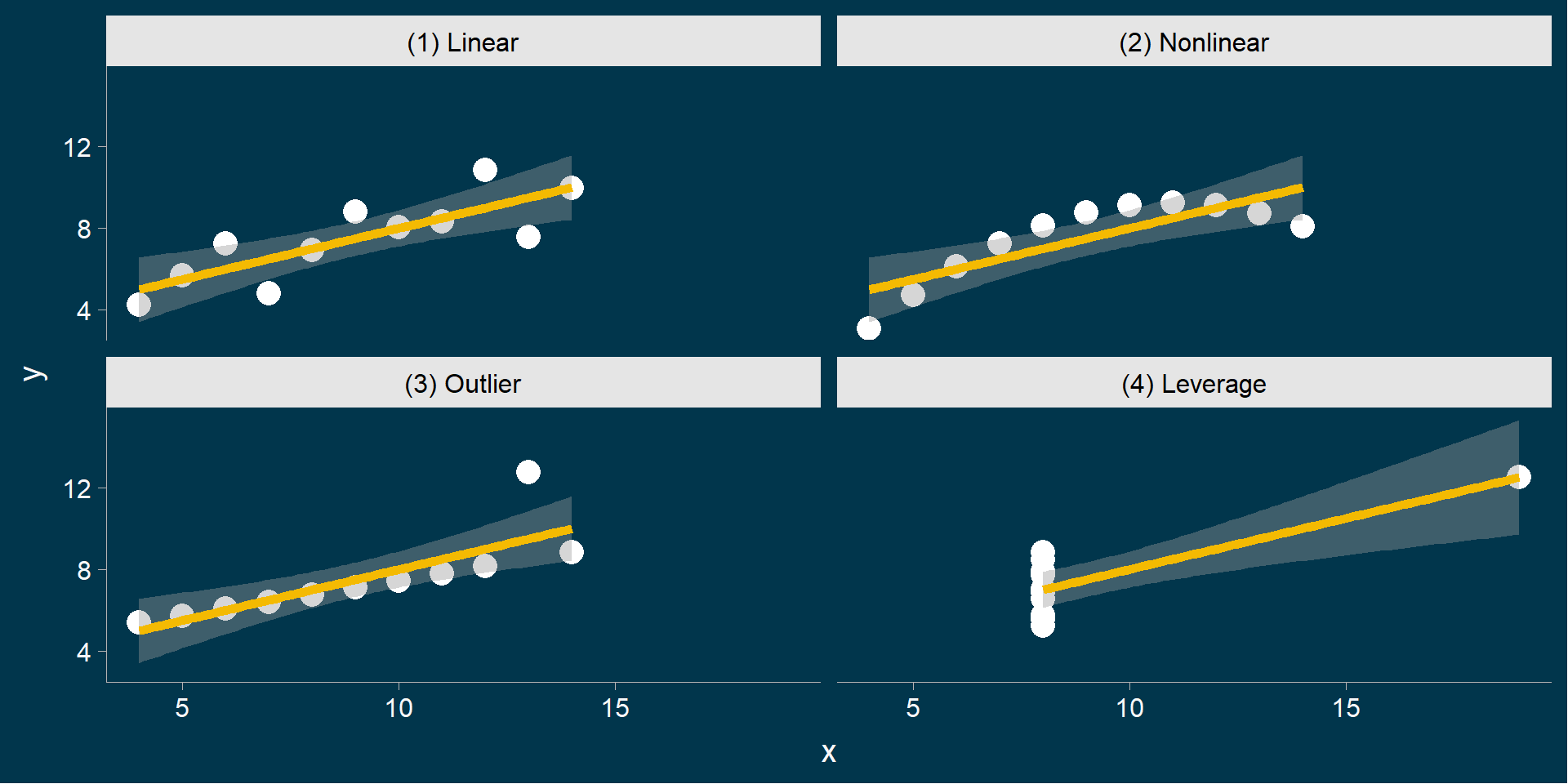
Šta je statistička kontrola?

N <- 300

primer <- tibble(
  pridruzena_varijabla = sample(0:1, N, replace = TRUE),
  prediktor = runif(N, 0 , 1) + (0.3 * pridruzena_varijabla),
  ishod = 2.0 + (0.5 * prediktor) + (0.25 * pridruzena_varijabla)
)

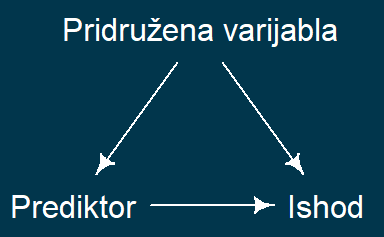
pridruzena_varijabla	prediktor	ishod
0	0.9336965	2.466848
1	0.8425316	2.671266
0	0.2194225	2.109711
1	0.7894278	2.644714
1	1.1011487	2.800574
1	0.7076307	2.603815

Kontrolisanje putem regresije

lm(ishod ~ prediktor, data = primer)

Call:
lm(formula = ishod ~ prediktor, data = primer)

Coefficients:
(Intercept)    prediktor  
     2.0076       0.6929  

lm(ishod ~ prediktor + pridruzena_varijabla, data = primer)

Call:
lm(formula = ishod ~ prediktor + pridruzena_varijabla, data = primer)

Coefficients:
         (Intercept)             prediktor  pridruzena_varijabla  
                2.00                  0.50                  0.25  

Vežba: linearna regresija

Koristeći dopunjenu bazu DZ odgovori na sledeća istraživačka pitanja:

1. Da li postoji povezanost između sistolne tenzije i

ukupnog holesterola?

2. Za ispitanika sa ukupnim holesterolom od 6.2 mmol/l

izračunaj vrednost sistolne tenzije (mmmHg).

Korelacija vs. regresija

• Korelacija opisuje povezanost između varijabli, ne određuje najbolju liniju
• Kod korelacije nije potrebno razmišljati o uzrocima
• Kod regresije \(Y\) \(\rightarrow\) \(X\) \(\not =\) \(Y\) \(\leftarrow\) \(X\)

Struktura kursa

Nedelja	Tema
1	Uvod u medicinsku statistiku
2	Sređivanje podataka
3	Statističko opisivanje podataka
4	Verovatnoća i raspodele verovatnoća
5	Populacija i uzorak
6	Testiranje hipoteza o populacionim prosečnim vrednostima i proporcijama
7	Testiranje hipoteza o učestalostima
8	Testiranje hipoteza o rangovima
9	Korelacija
10	Regresija / Kolokvijum
11	Podaci, informacije i znanje
12	Zdravstveni informacioni sistem
13	Mere dijagnostičke tačnosti
14	Medicinsko odlučivanje
15	Bioinformatika