Hypothesis Testing based on Rank Order
Dr Nikola Grubor
2024-11-20
Parametric and non-parametric tests
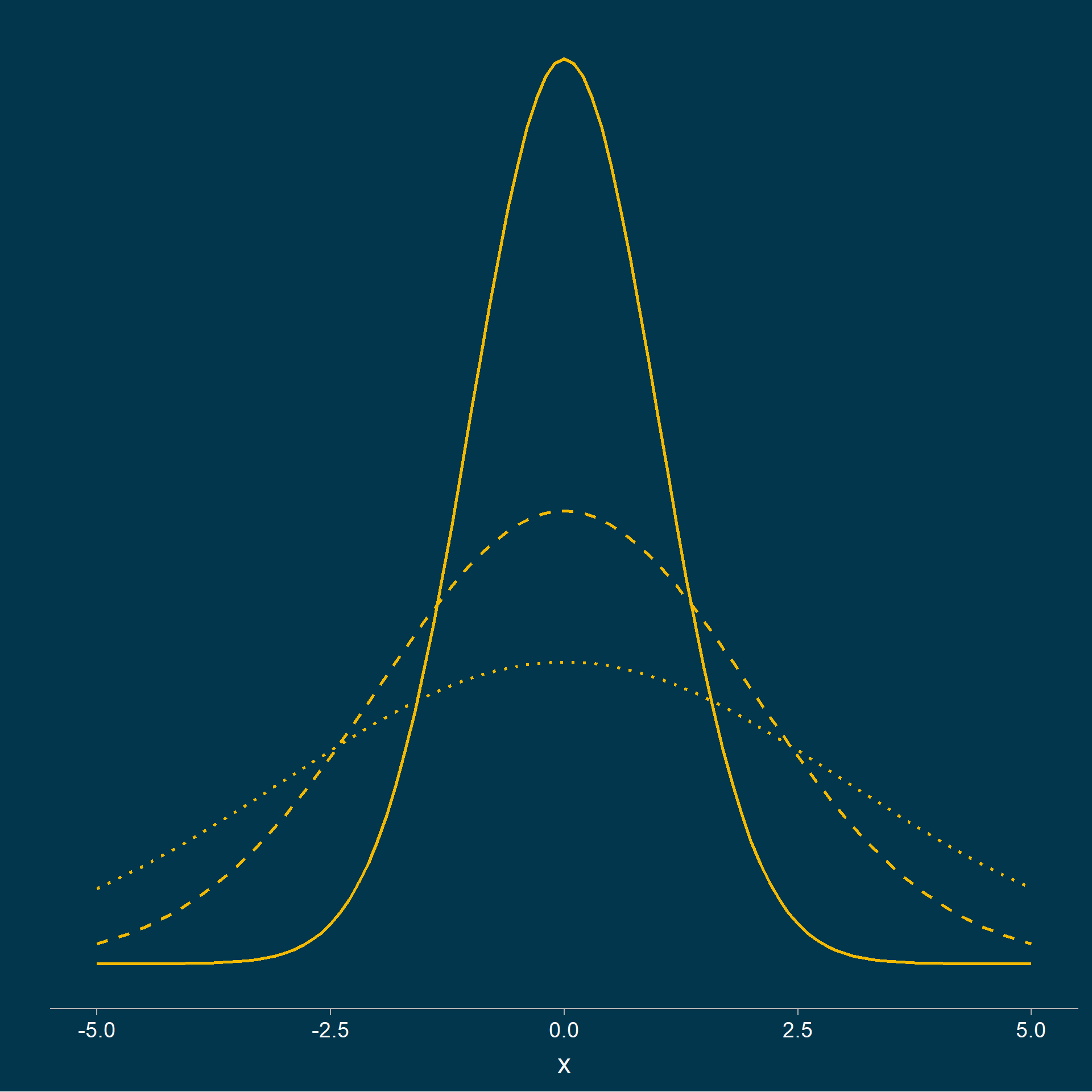
- Tests comparing arithmetic means assume a normal distribution
- The normal distribution is defined by parameters: mean and standard deviation
- Tests that do not rely on distributions are called non-parametric
A recipe for testing the null hypothesis
- Form a hypothesis before seeing the data
- Determine the null and alternative hypothesis
- Collect relevant data
- Create a model that represents the data and calculate the test statistic
- Calculate the probability that our data gives the obtained test statistic if the null is true
- Assess “statistical significance”
Why use ranks?
- Fewer assumptions are better
- Normality rarely holds
- When assumptions are violated, obtained p-values are wrong
Important
We lose statistical power if the data actually meet the conditions for a parametric (eg., Student’s) test

Mann-Whitney U / Wilcoxon rank-sum test
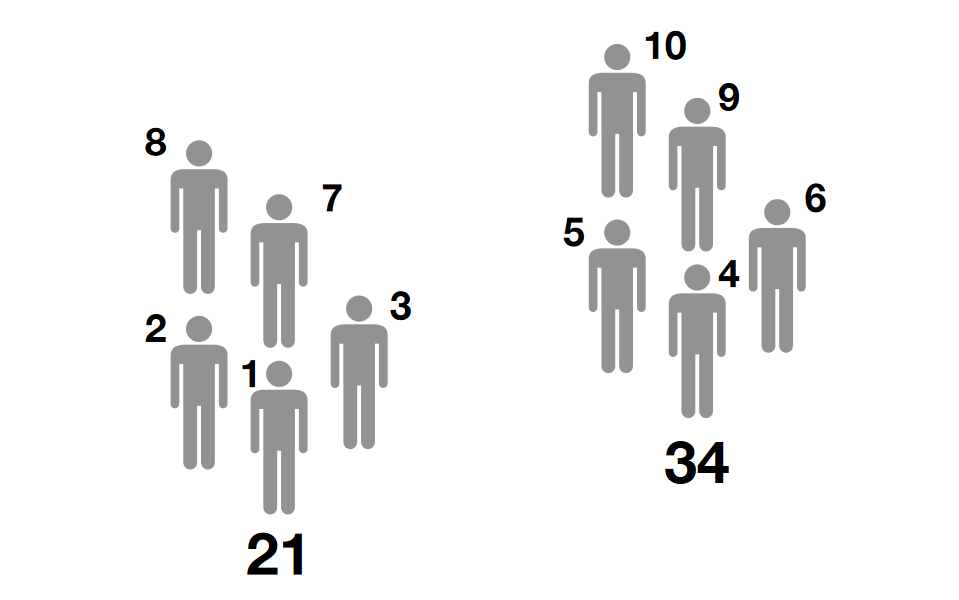
Assumptions of the rank sum test
Input:
- Numerical non-normal data, ordinal data
Assumptions:
- The sample consists of independent observations
- Data can be ranked
Important
It has less statistical power than parametric tests, if the conditions for parametric tests are met.
Checking for normality
- Coefficient of Variation
- Skew and Kurtosis
- QQ Plot
- Histogram
- Statistical tests for normality
Exercise: MWW test
Examine whether people with different
altitudes of residence
differ according to the concentration of fibrinogen.

Wilcoxon signed rank test
Input:
- Numerical non-normal data, ordinal data
Assumptions:
- The sample consists of dependent observations
- Data can be ranked
Exercise: Wilcoxon signed rank test
The database Depresion.xlsx
contains pre- and post treatment
depressive symptom measurements.
Did the treatment affect them?
Statistical test selection
- One or two samples
- Repeated measurements or not
- Data type (numeric, ordinal, categorical)
- Use data summaries to determine whether the data meet the normality assumption
