Testiranje hipoteza o učestalostima

Dr Nikola Grubor

2024-11-12

Problem očekivanih proporcija

Da li mogu da proverim da li su me prevarili za boju M&M bombona ako očekujem da ih u kesici ima međusobno jednak broj?

tinytable_kzc6k0z0o1vd7uzjjjn8
Boja Broj
Crvene 30
Plave 33
Zelene 37

Pirsonov hi-kvardrat test slaganja

tinytable_zdna6ctd5r45c5bc92tz
Boja Broj Očekivanje Kv. razlika Hi-kvadrat promenljiva
Crvene 30 33.333 11.109 0.333
Plave 33 33.333 0.111 0.003
Zelene 37 33.333 13.447 0.403

\[ \chi^2 = \sum\frac{(O_i - E_i)^2}{E_i} = 0.333 + 0.003 + 0.403 = 0.739\]

Hi-kvadrat raspodela

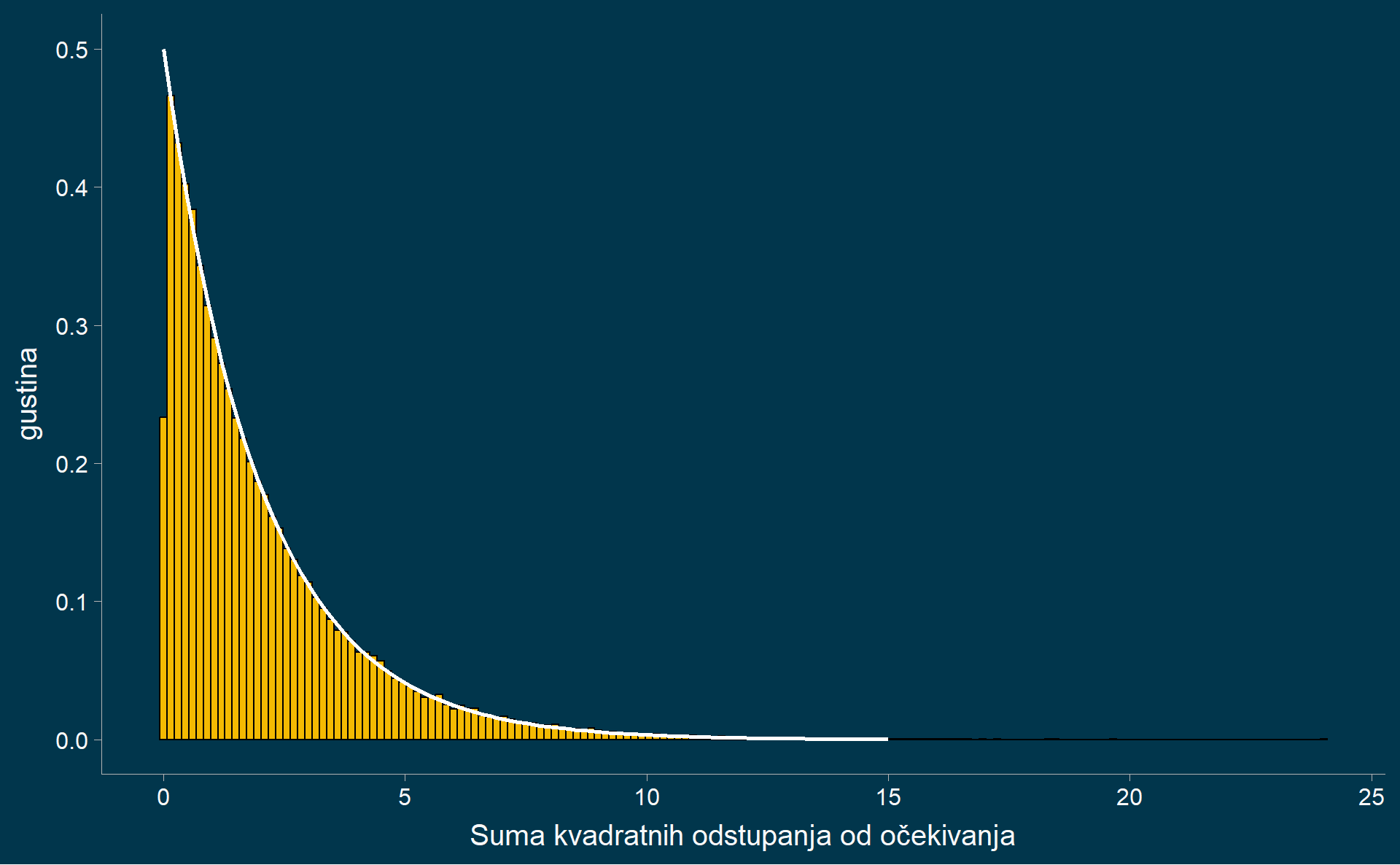
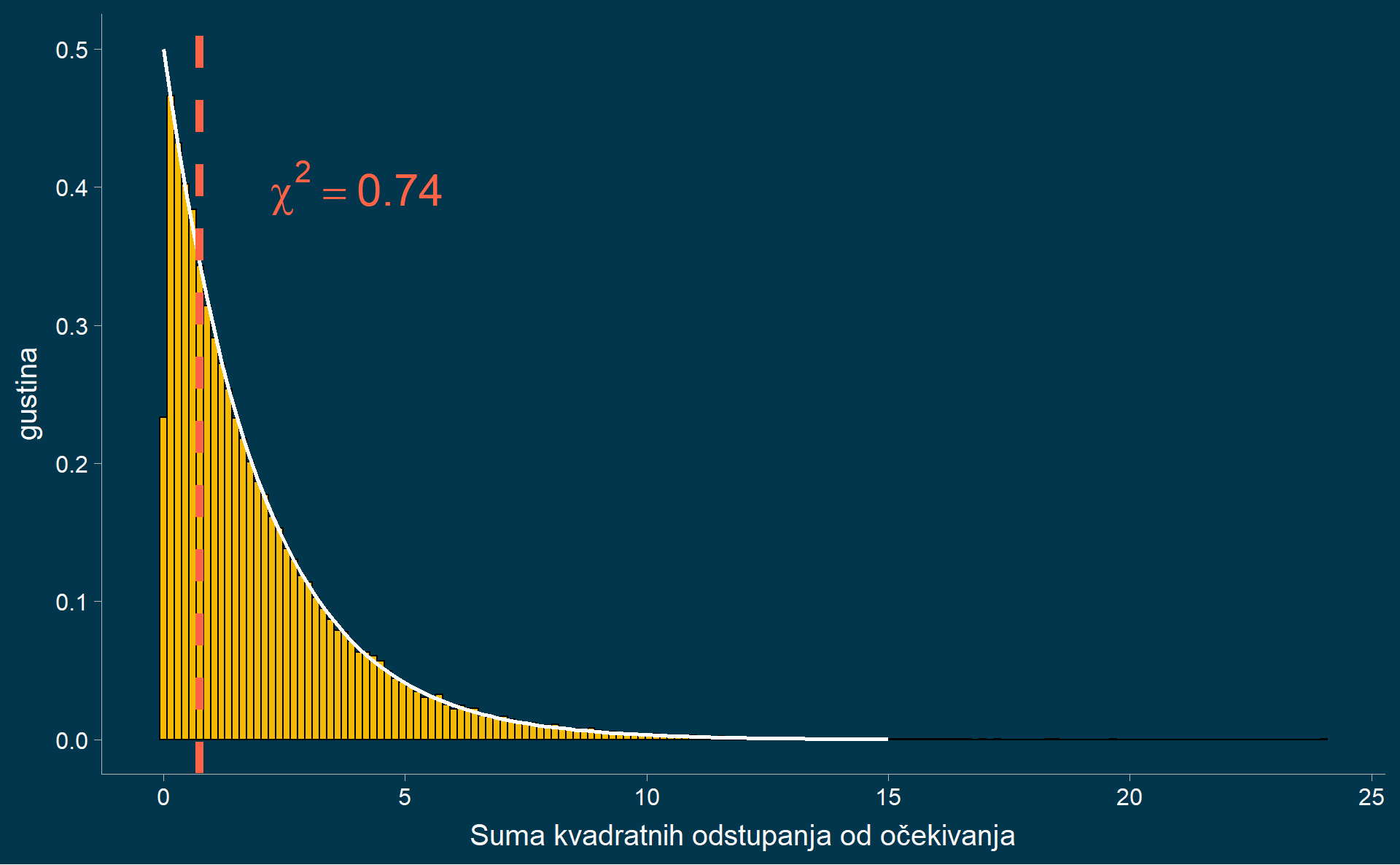
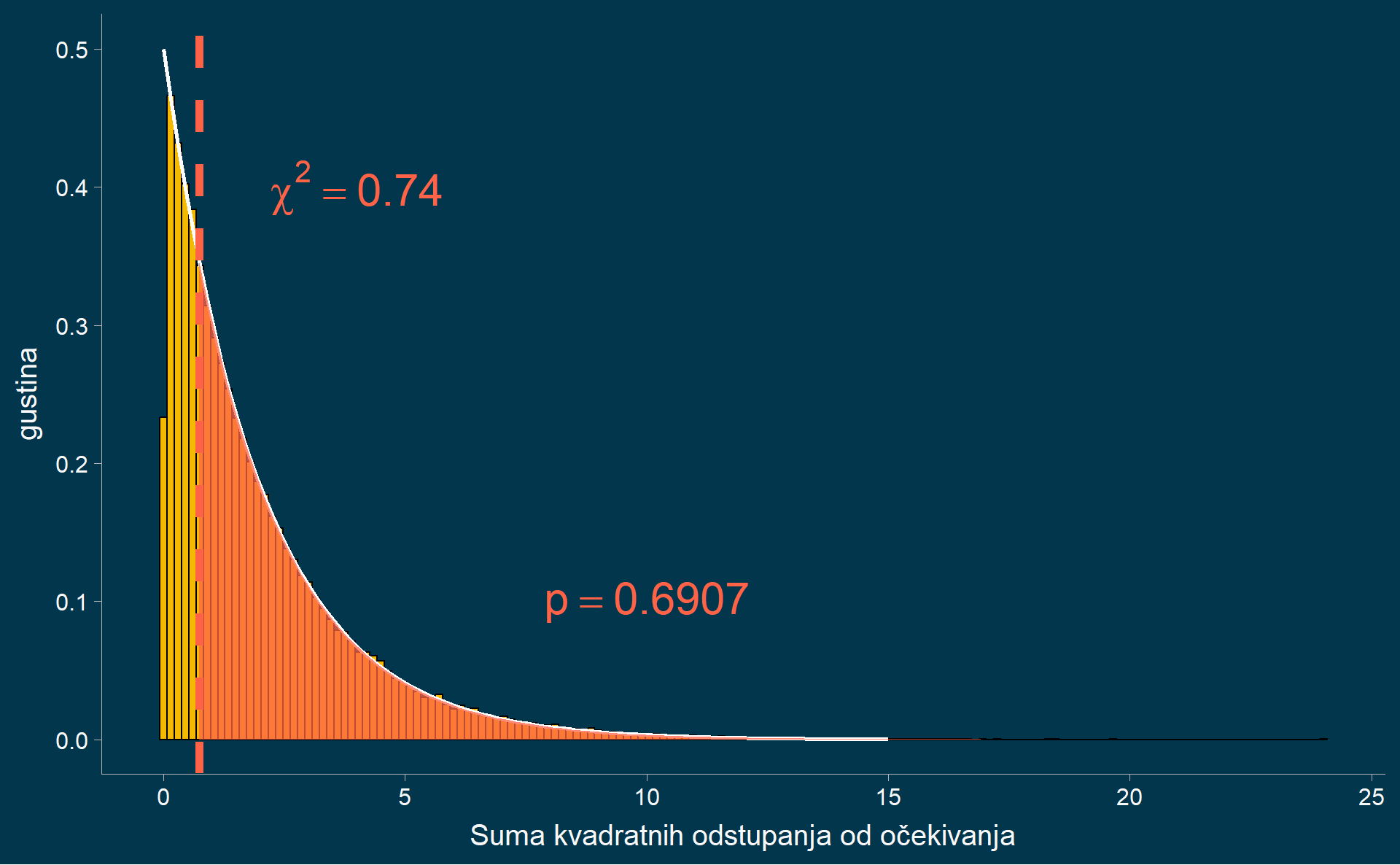
Interpretacija hi-kvadratnog testa slaganja

chisq.test(x = c(30, 33, 37), p = c(33, 33, 33), rescale.p = TRUE)

    Chi-squared test for given probabilities

data:  c(30, 33, 37)
X-squared = 0.74, df = 2, p-value = 0.6907

\(H_0:\) Proporcije opserviranih kategorija se ne razlikuju od teoretskih proporcija.

\(H_1:\) Proporcije opserviranih kategorija se razlikuju od teoretskih proporcija.

“Proporcije testiranih kategorija se statistički značajno ne razlikuju od teoretskih proporcija.”

Vežba: očekivane vrednosti ABO krvne grupe

  • Proveriti da li se opservirane učestalosti ABO krvnih grupa datih u tabeli razlikuju od očvekivanih
tinytable_aj53uh4tqvrh16b6gtsj
A B AB O
Učestalost 59 19 7 55

Očekivane učestalosti su:

O: 44.5%, A: 38.9%, B: 12.1%, AB: 4.5%

Asocijacija između dve kategorije?

Problem: Da li je nodularnost konture jetre povezana sa konzumiranjem alkohola?

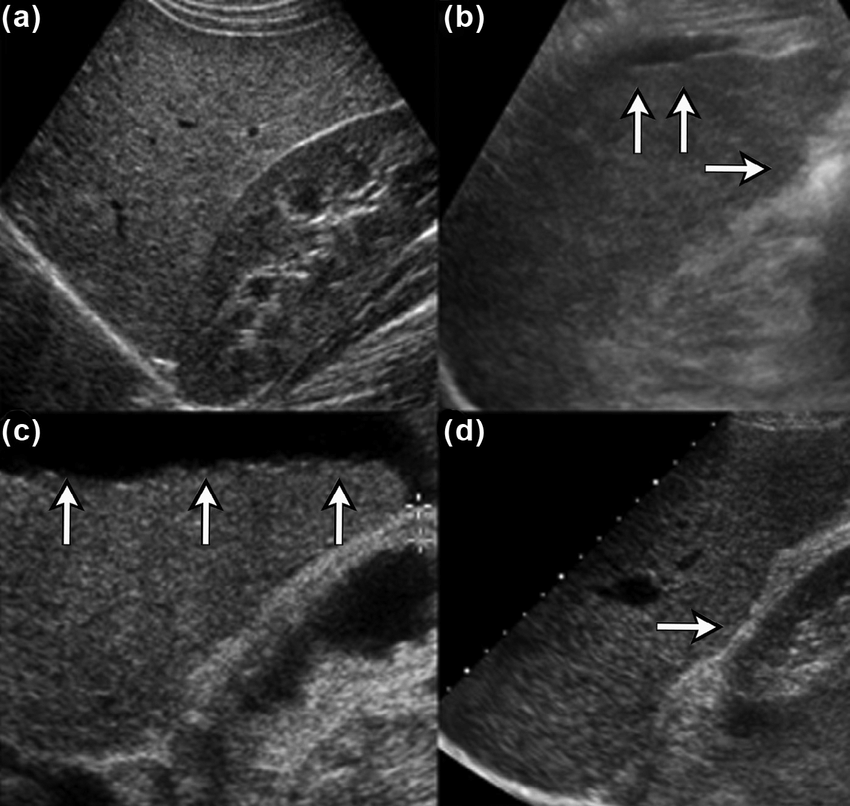
Tabela kontigencije kao preduslov za test

  • Standardan način prikazivanja kategorijalnih podataka je preko tabele kontigencije.

  • Predstavlja broj (ili proporciju) opservacija koje pripadaju svim mogućim kombinacijama kategorija.

tinytable_sifw512kijvwxxatwezs
Nodularne promene Alkohol: Da Alkohol: Ne
Ne 16 79
Da 10 13

Obično je lakše tumačiti proporcije

tinytable_pwyjz5ufz0a8ir5mdc6s
Nodularne promene Alkohol: Da Alkohol: Ne
Ne 16 79
Da 10 13
tinytable_c007d7d7av5ja6i2lzl8
Nodularne promene Alkohol: Da (proporcija) Alkohol: Ne (proporcija)
Ne 0.17 0.83
Da 0.43 0.57

Kako da odredimo očekivane učestalosti

  • Pirsonov hi-kvadrat test nam omogućava da testiramo da li se opservirane učestalosti razlikuju od očekivanih
  • Treba da odredimo koje učestalosti očekujemo ako kategorije nisu međusobno povezane (nezavisne su)

Možemo se poslužiti osobinom verovatnoće:

\[ P(X \cap Y) = P(X) \times P(Y) \]

Ručno računanje očekivanih učestalosti

tinytable_vsjsa8apgl4aa5pxp9g0
Nodularne promene Alkohol: Da Alkohol: Ne Margina
Ne P(Bez nodularnih)*P(Alkohol) P(Bez nodularnih)*P(Bez Alkohola) P(Bez nodularnih)
Da P(Nodularne)*P(Alkohol) P(Nodularne)*P(Bez Alkohola) P(Nodularne)
Margina P(Alkohol) P(Bez Alkohola) Ukupno

Interpretacija Pirsonovog hi-kvadrat testa za r \(\times\) k tabele (1)

rezultati <- chisq.test(nodularnost_dat, correct = FALSE)
rezultati

    Pearson's Chi-squared test

data:  nodularnost_dat
X-squared = 7.6474, df = 1, p-value = 0.005685

“Postoji statistički značajna asocijacija između nodularne konture jetre i konzumiranja alkohola.”

Interpretacija Pirsonovog hi-kvadrat testa za r \(\times\) k tabele (2)

Opservacije (originalni podaci):

           Alkohol
Nodularnost Da Ne
         Ne 16 79
         Da 10 13

Očekivani podaci (svi moraju biti \(>5\)):

           Alkohol
Nodularnost        Da      Ne
         Ne 20.932203 74.0678
         Da  5.067797 17.9322

Vežba: Pirsonov hi-kvadrat test za r \(\times\) k tabele

  • Uneti sledeće opservacije i interpretirati rezultat
tinytable_0t07byi81rf5c723g9ae
Pacijent Tonzilektomija Bez tonzilektomije
Hodžkinova bolest 41 44
Kontrola 33 52

McNemarov test

  • McNemarov test je metod za testiranje dva vezana (zavisna) uzorka
  • Iste jedinice su opservirane više puta
  • Mečovane jedinice dva uzorka
tinytable_dffd30624q5q5v45qkml
Test 2 + Test 2 -
Test 1 + a b
Test 1 - c d

\[ \chi^2 = \frac{(b - c)^2}{b + c} \]

Interpretacija McNemarovog testa

\(H_0:\) Tabela kontigencije je simetrična.

\(H_1:\) Tabela kontigencije nije simetrična.

tinytable_7okhu56gr6jhsgw11cn2
pre posle
0 1
1 1
0 1

Tabela kontigencije za parove:

   posle
pre  0  1
  0 18 35
  1 13 34

Rezultat:


    McNemar's Chi-squared test

data:  .
McNemar's chi-squared = 10.083, df = 1, p-value = 0.001496

Vežba: McNemarov test

  • Preuzeti i analizirati bazu podataka Aritmije.xlsx
  • Interpretirati rezultat

Fisherov test tačne verovatnoće

  • Može se koristiti uvek
  • Konzervativan je, te se koristi samo ako se ne može upotrebiti hi-kvadrat test
  • Uslovljen je marginama*

\[ p = \frac{(a+b)!\,(c+d)!\,(a+c)!\,(b+d)!}{n!\,a!\,b!\,c!\,d!} \]

Žena koja pije čaj

tinytable_lflswu7ntmvgpmpz7ez2
Mleko prvo Čaj prvo Ukupno
Pogađala Mleko 4 0 4
Pogađala Čaj 0 4 4
Ukupno 4 4 8 

    Fisher's Exact Test for Count Data

data:  tea_data
p-value = 0.01429
alternative hypothesis: true odds ratio is greater than 1
95 percent confidence interval:
 2.003768      Inf
sample estimates:
odds ratio 
       Inf

Vežba: Fisherov test tačne verovatnoće

  1. Preuzeti i analizirati bazu podataka Alkohol i hipertenzija.xlsx
  2. Interpretirati rezultat

Biranje testa (do sad)

tinytable_zqm2e6xuhhy8eg6t708y
Tip testa Parametarski Neparametarski
Jedan uzorak t-test za jedan uzorak hi-kvadrat test slaganja
Dva nezavisna t-test hi-kvadrat/Fisherov test
Dva zavisna t-test za zavisne McNemarov test

Struktura kursa

tinytable_cycd3osf8llndtu7d0mp
Nedelja Tema
1 Uvod u medicinsku statistiku
2 Sređivanje podataka
3 Statističko opisivanje podataka
4 Verovatnoća i raspodele verovatnoća
5 Populacija i uzorak
6 Testiranje hipoteza o populacionim prosečnim vrednostima i proporcijama
7 Testiranje hipoteza o učestalostima
8 Testiranje hipoteza o rangovima
9 Korelacija
10 Regresija / Kolokvijum
11 Podaci, informacije i znanje
12 Zdravstveni informacioni sistem
13 Mere dijagnostičke tačnosti
14 Medicinsko odlučivanje
15 Bioinformatika