Medicinska statistika i informatika

Zašto uzorkujemo

Ograničenja: vreme i novac.
Kako da zaključimo ispravno, a da nismo videli svaki primer onoga što nas interesuje?

Urgentno lečenje septičnog šoka

Sepsa ima ogroman mortalitet. Kako da je lečimo?

Kako da odgovorimo na ovo pitanje?

Osnovni termini

Populacija (skup svih istovrsnih elemenata)
- Ciljna populacija (skup elemenata za koji generalizujemo)
Uzoracka populacija (populacija koja je dostupna)
Uzorak (podskup osnovnog skupa (populacije) izabran na osnovu kriterijuma)

Istraživačko pitanje vs. ciljna grupa

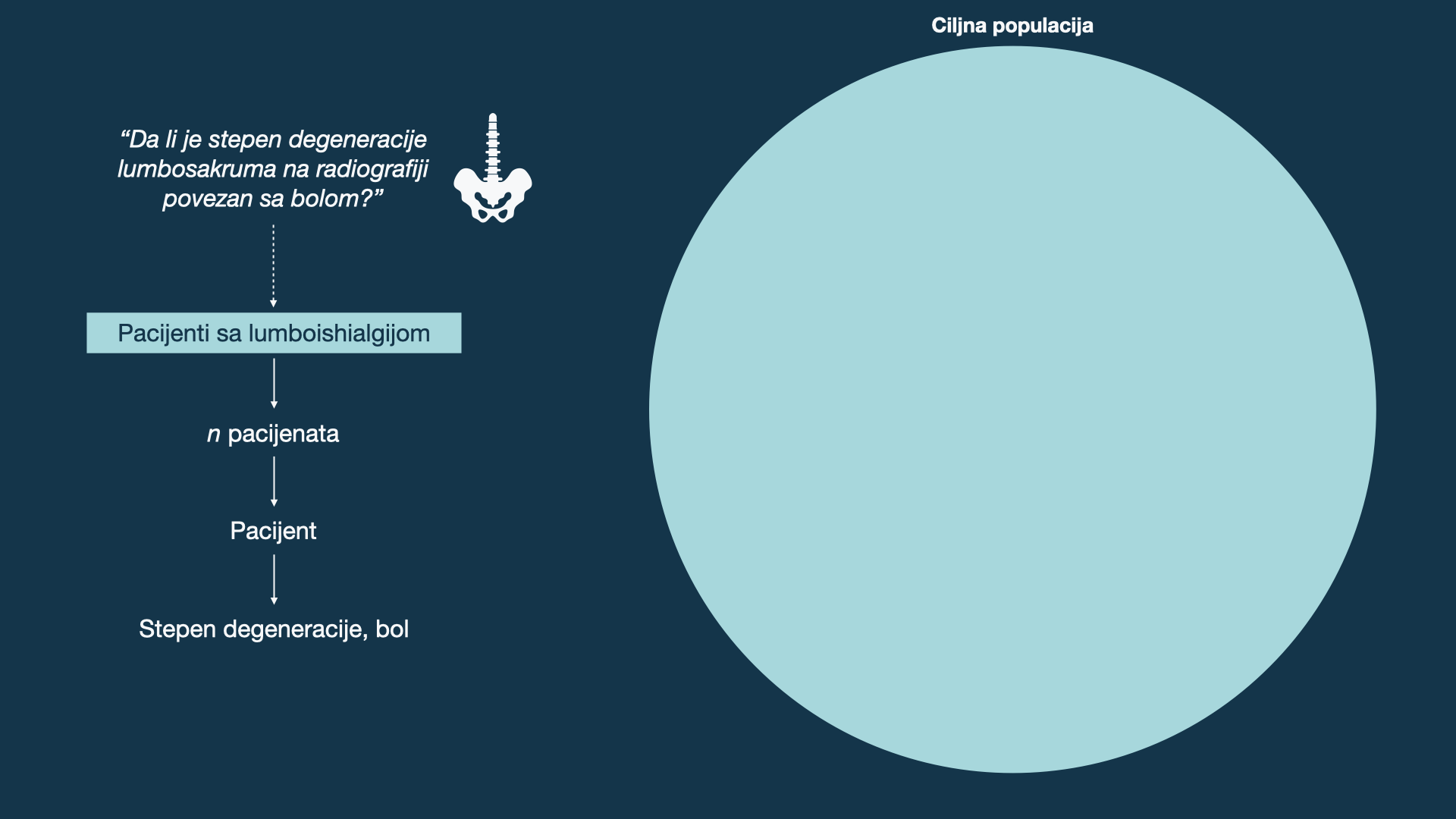
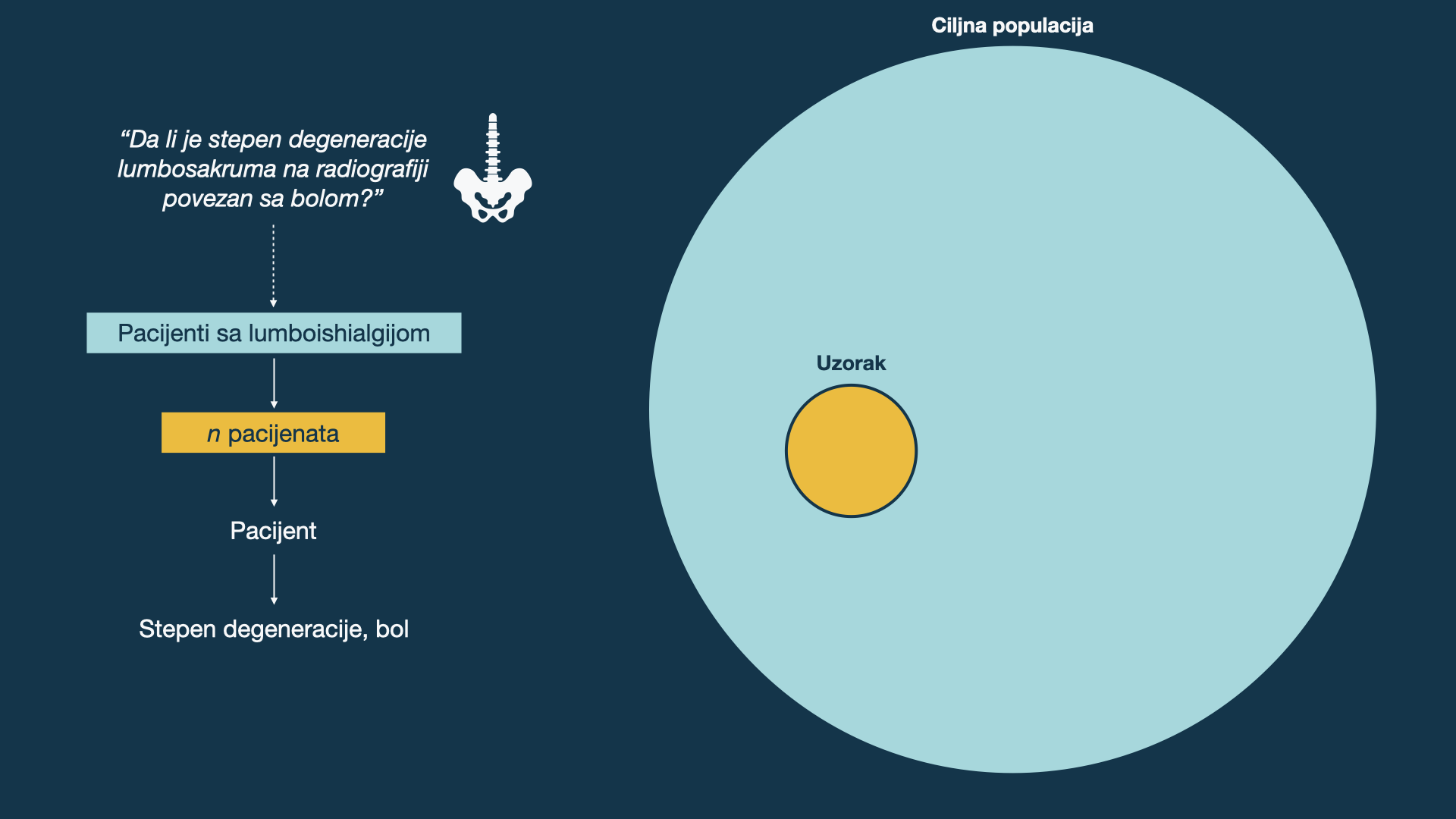
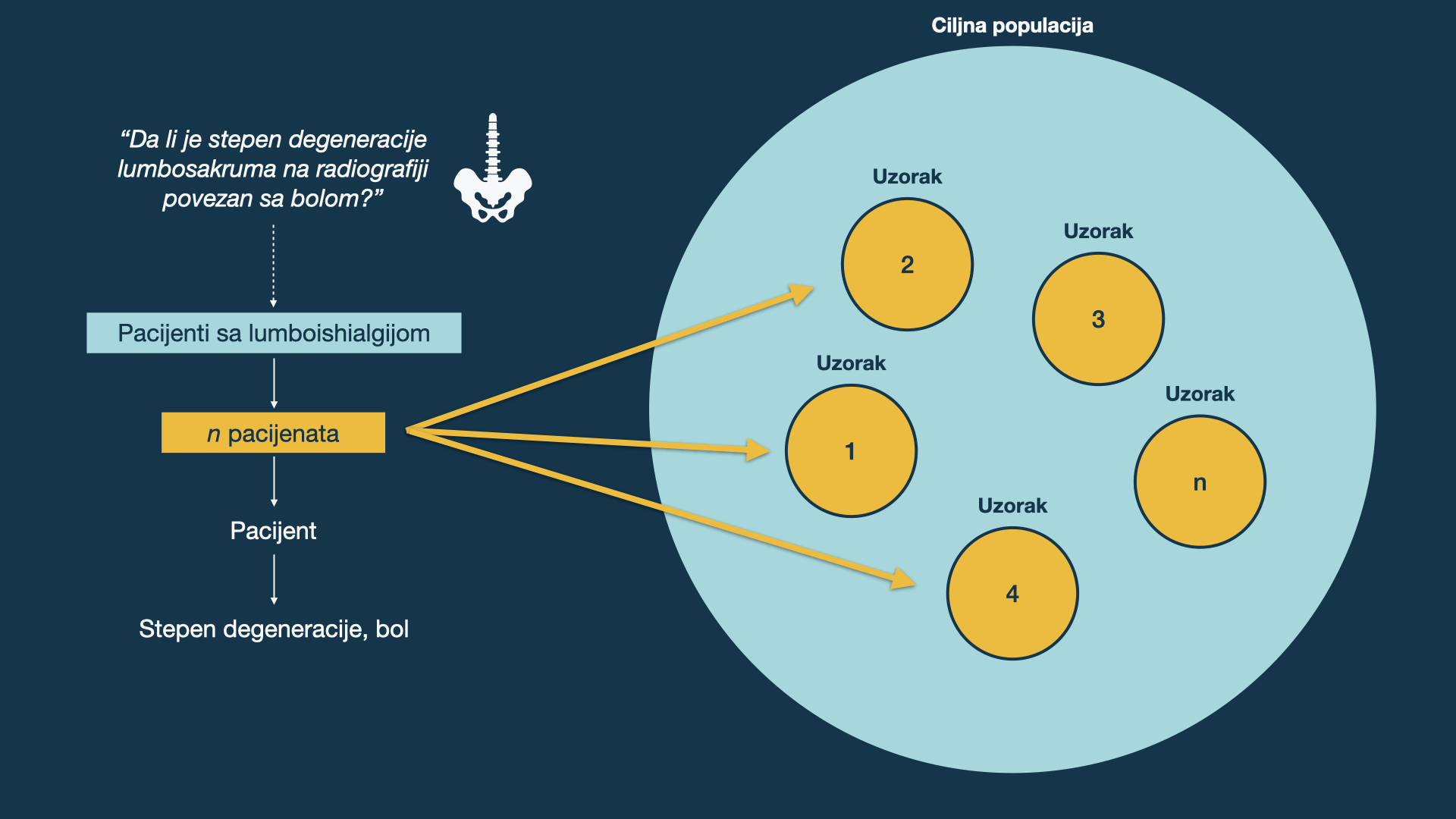
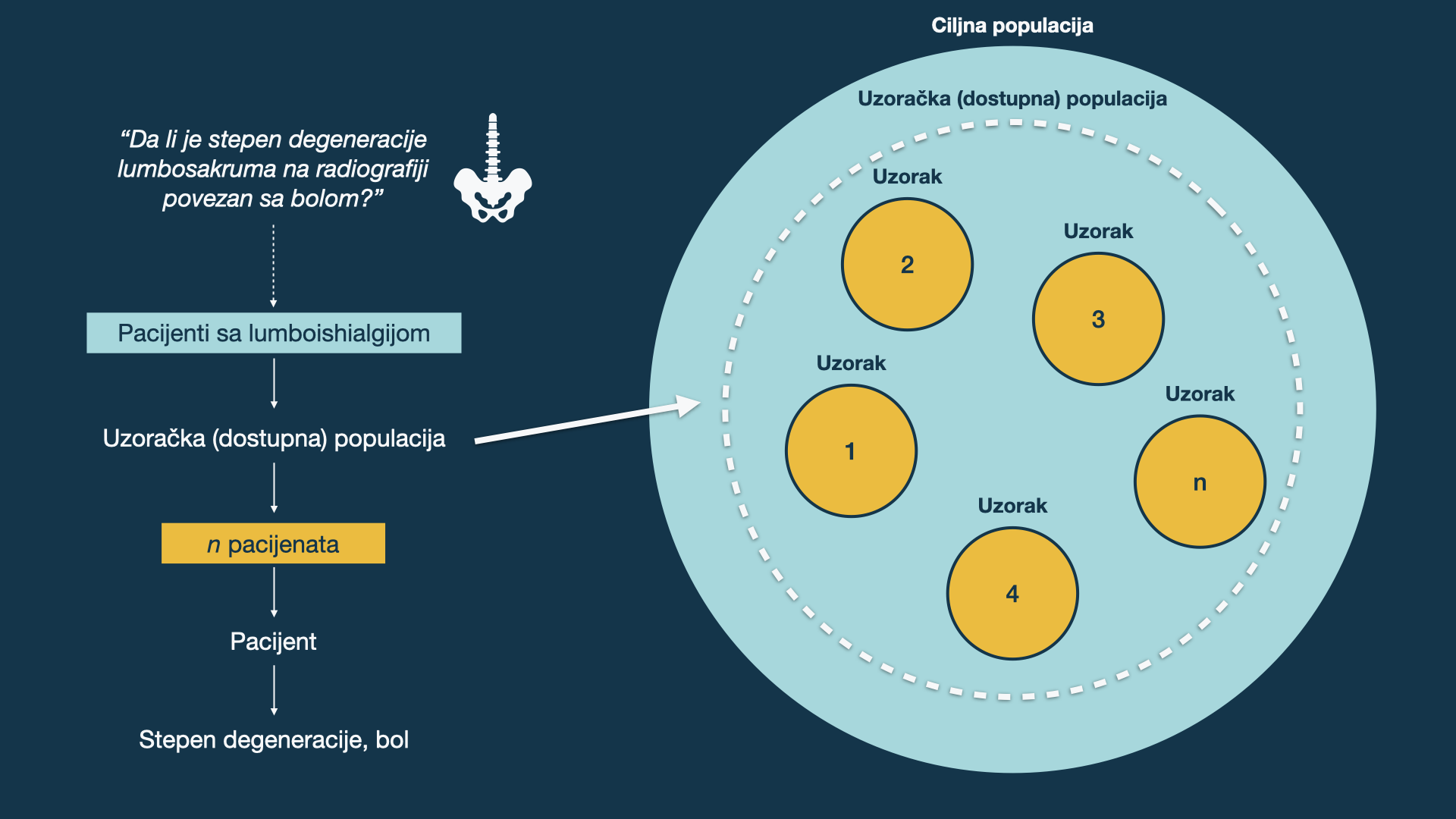
Kako se dostupna populacija razlikuje?

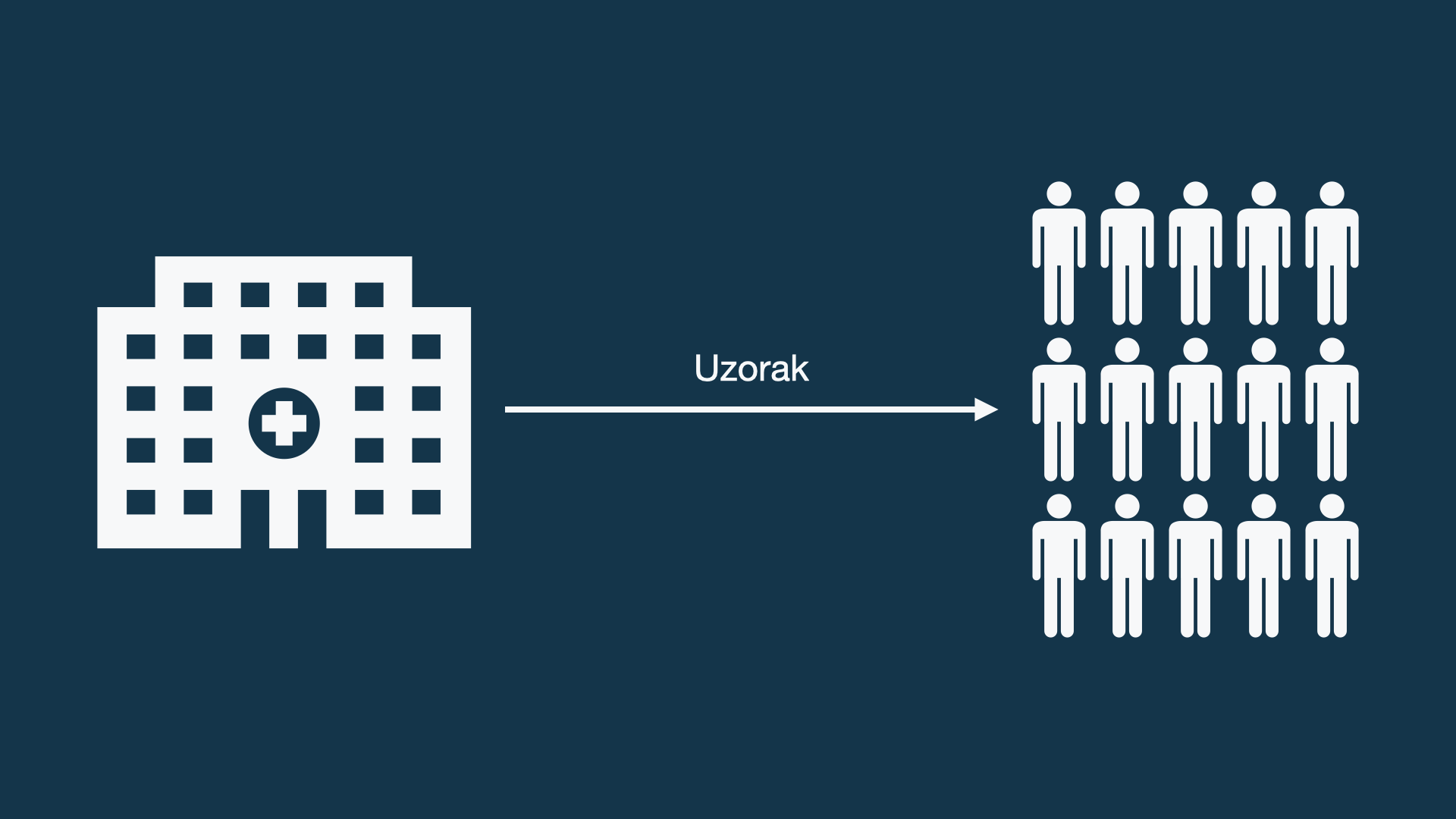
Pogrešna slika realnosti

Izbor jedinica posmatranja mora biti nezavisan od posmatranog obeležja.
Verovatnoća odabira jedinica posmatranja mora biti unapred poznata.

Pristrastnost

Statistička pristrastnost: Kada metod pokazuje netačnu, iskrivljenu sliku realnosti.

Žašto randomizujemo?

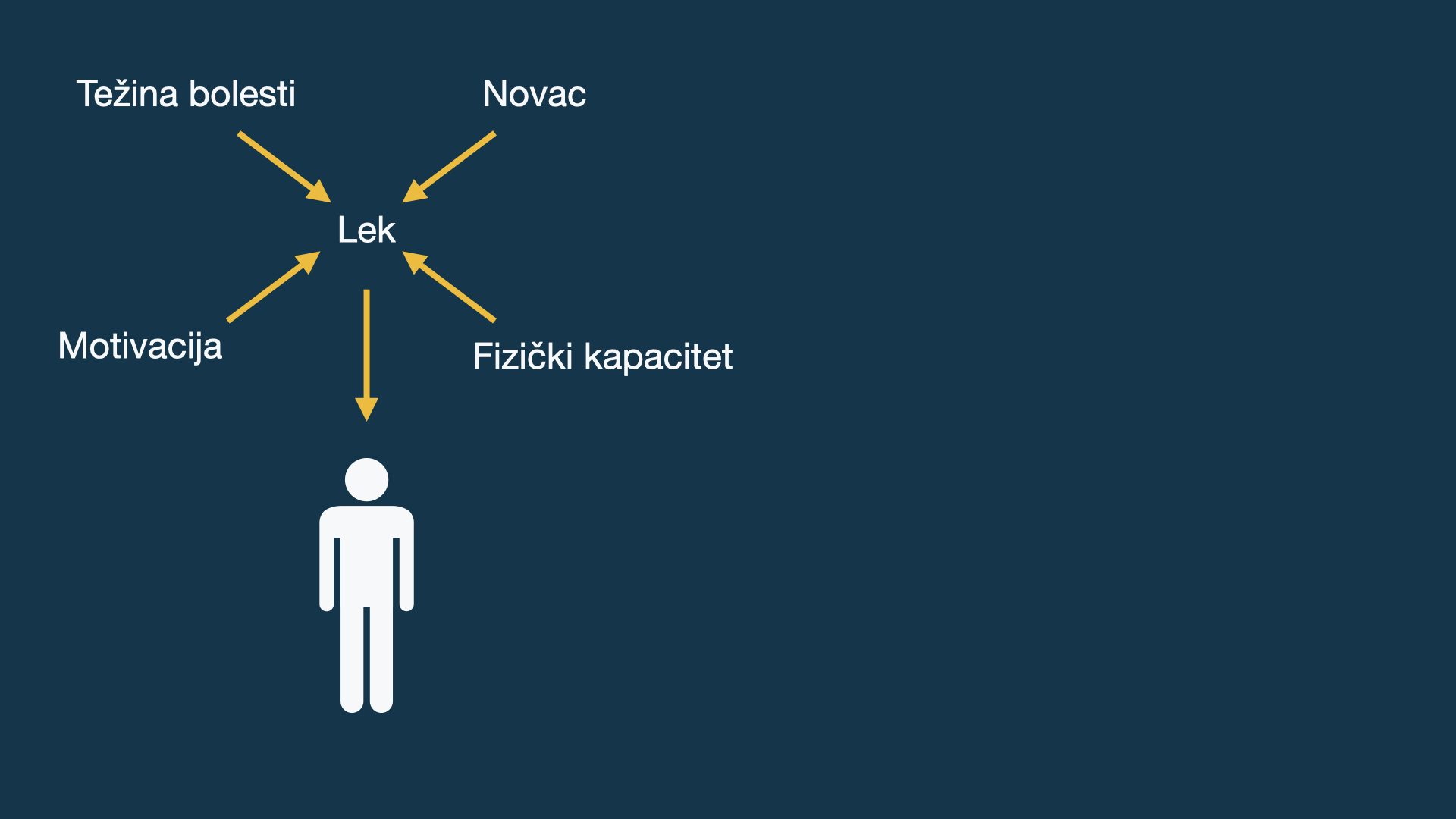
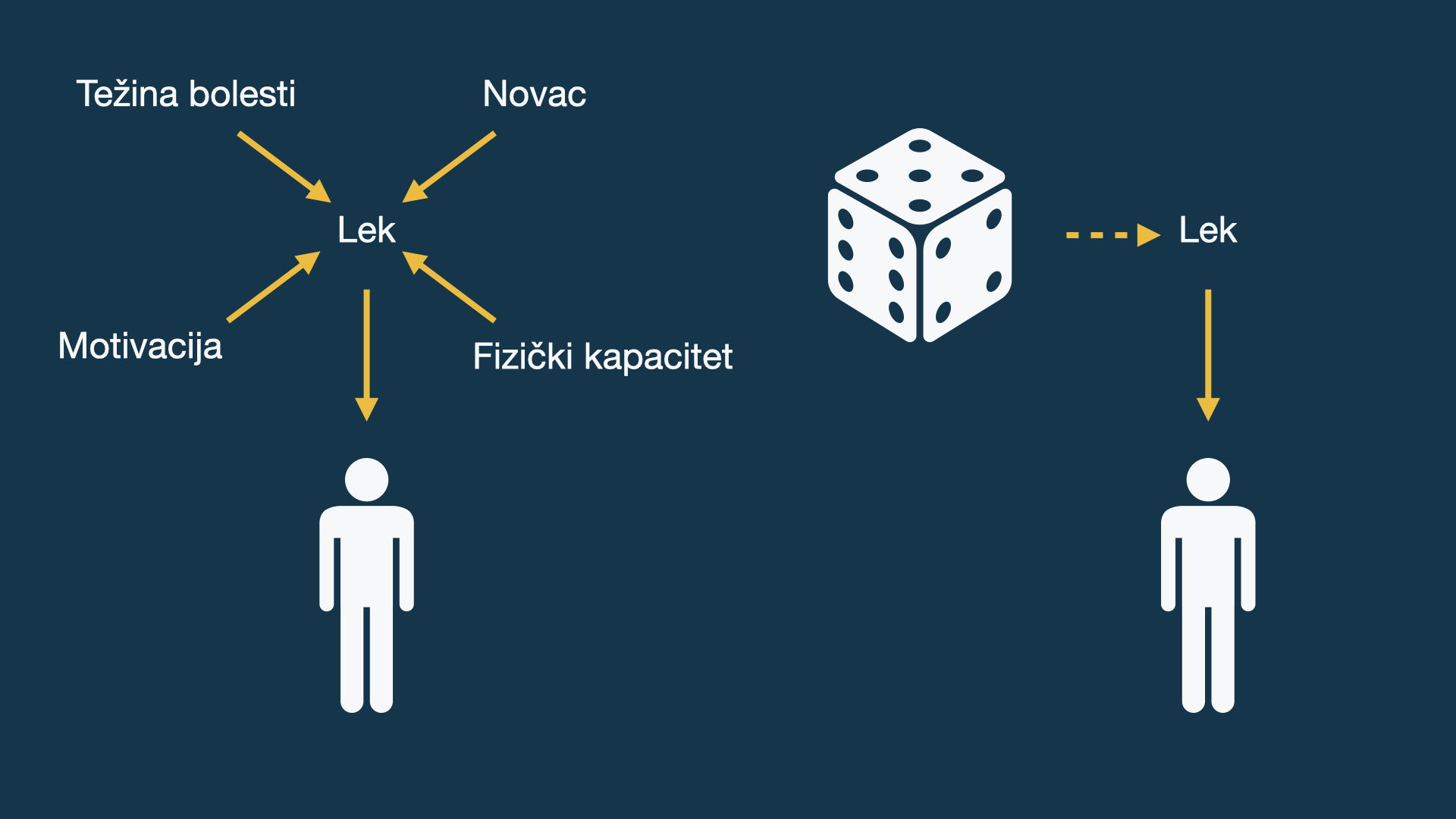
Vrste uzoraka

Uzorački okvir: Spisak ili lista svih elemenata populacije koju želimo da uzorkujemo.

Slučajni uzorak
- Tačno znamo verovatnoću da neko bude izabran
Neslučajni
- Može biti pristrasan

Slučajni uzorci

Prost
Sistematski
Stratifikovani
Klaster

Prost slučajan uzorak

Najjednostavniji oblik uzorkovanja. Bira se $n$ jedinica iz izmešane populacije (npr. uzorak krvi).

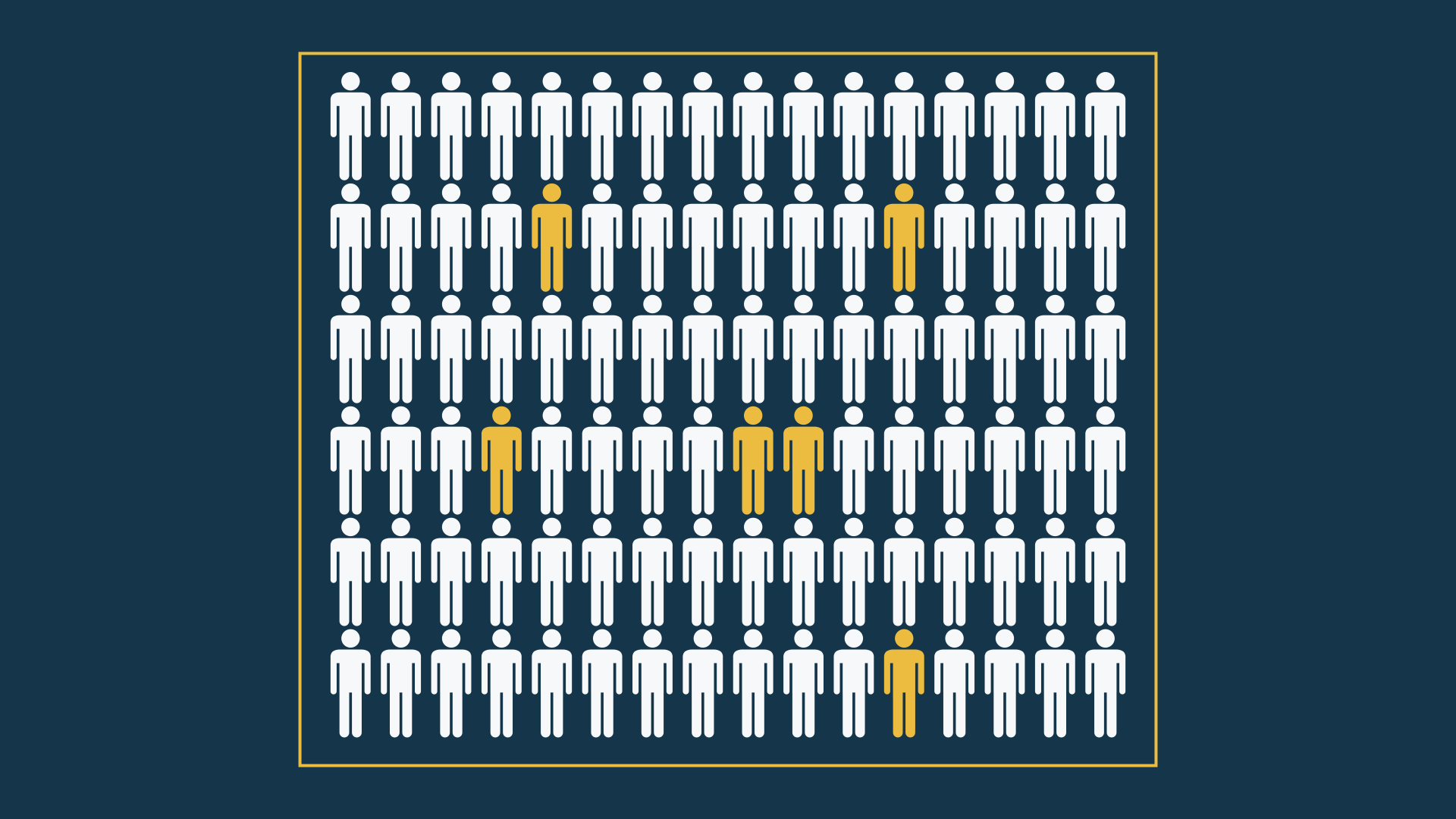
Sistematski slučajan uzorak

Koristi se kao zamena za prost slučajan uzorak kada nemamo spisak jedinica ili je spisak nasumičnog redosleda.

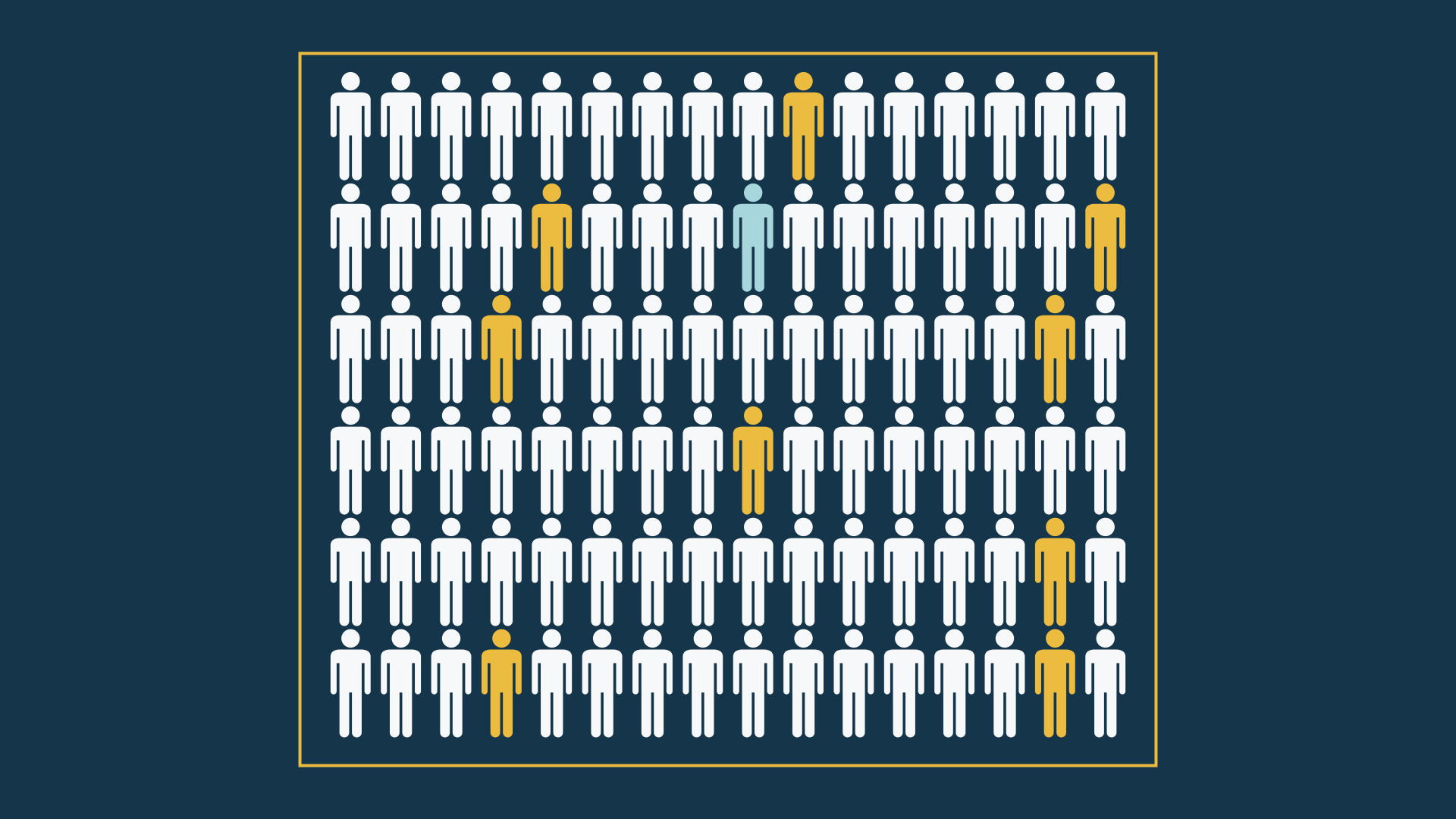
Klaster slučajan uzorak

Koristan kada nemamo definisan uzorački okvir ili nas zanima opsežna populacija koju nije lako uzorkovati.

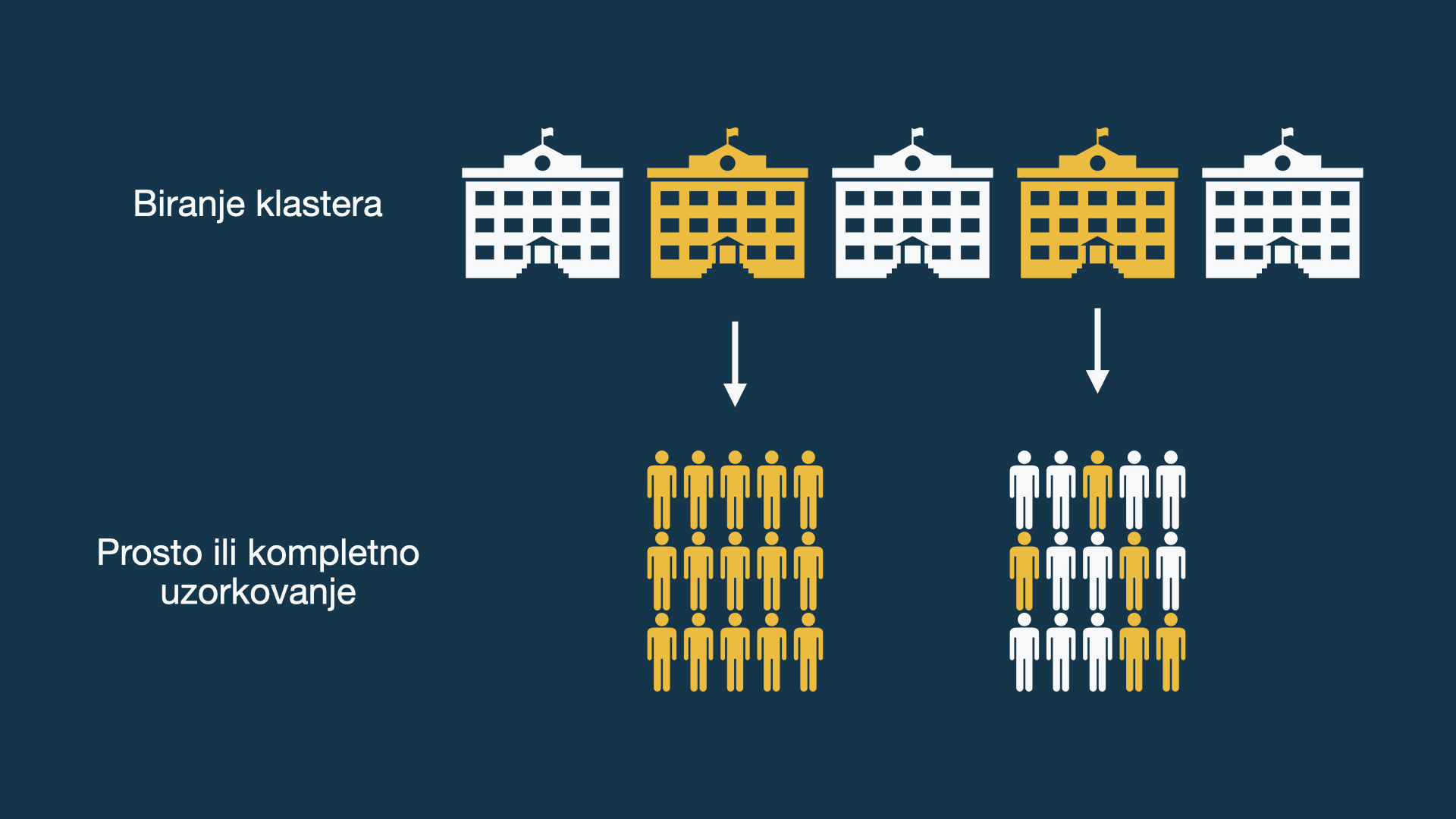
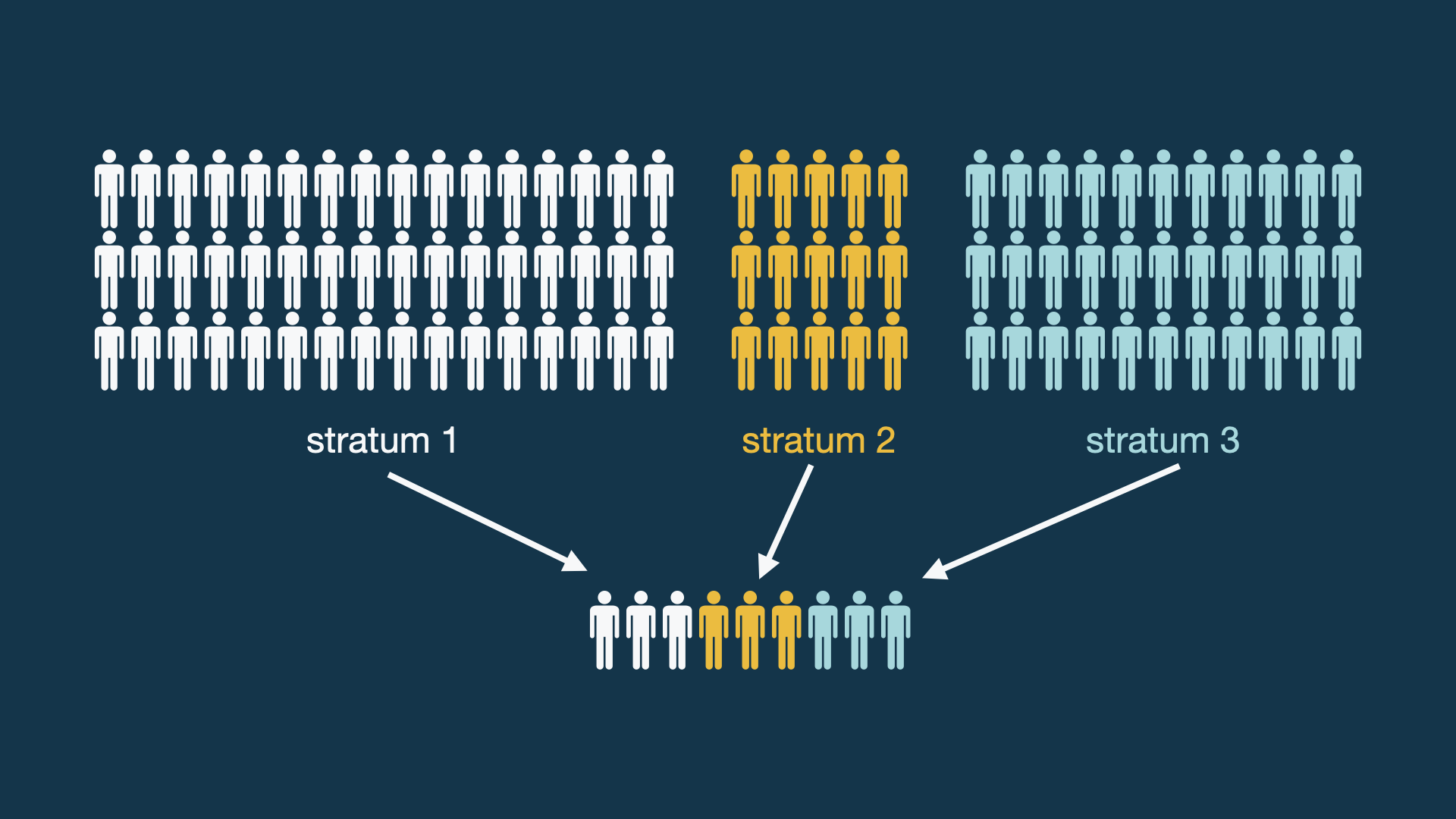
Stratifikovan slučajan uzorak

Populacija se deli na stratume od interesa. Jedinice (birane prostim slučajnim uzorkovanjem) unutar stratuma su međusobno sličnije.

Neslučajni uzorci

Prigodan
- Pacijenti na odeljenju
Kvota
- Kategorije → već određena kvota se ispunjava
Namerni
- Pilot studija (inovacije)

Vežba: uzorkovanje

Iz baze “Sistolni pritisak.xlsx” odrediti prost i sistematski uzorak veličine 10.

Prost:

sample(1:99, 10, replace = F)

 [1] 86 88  9 43  6 22 79 75 57 98

Sistematski:

sample(1:99, 1, replace = F)

[1] 9

Odrediti početnu jedinicu
- Korak $k = \frac{N}{n} = \frac{99}{10} \approx 10$
- Izabrati svaku 10-tu jedinicu

Problemi neslučajnih uzoraka

Postoji selekciona pristrasnost
Upitna valjanost generalizacije

Terminologija (i notacija)

tinytable_0rg20p0azh4dt9pfzkhd

	Populacija (parametar)	Uzorak (statistika)
Aritmetička sredina	$μ$	$\bar{x}$
Varijansa	$σ^{2}$	$s d^{2}$
Standardna devijacija	$σ$	$s d$
Proporcija	$π$	$p$

Mortalitet sepse i randomizacija

Kako bi ste randomizovali pacijente u JIL-u?

Dobili smo rezultat:

tinytable_6w4vh9a3duvpm9kqc2bh

Intervencija	Mortalitet	Ukupno	Stopa smrtnosti (%)
Agresivna terapija	92	439	21.0
Manje agresivna terapija	81	446	18.2

Da li je ovo dobra procena mortaliteta?

Greška uzorkovanja

Razlika između statistike izračunate na uzorku i parametra populacije.
Ponavljanjim uzorkovanjem možemo da saznamo raspodelu greške (uzoračka raspodela) statistike.

Standardna greška: Standardna greška je standardna devijacija uzoračke raspodele.

Standardna greška aritmetičke sredine i proporcije

Standardna greška aritmetičke sredine:

$S E_{\bar{x}} = \frac{s d}{\sqrt{n}}$

gde je: $s d$ , standardna devijacija statistike u uzorku (populaciona nije dostupna); $n$ broj opservacija.

Standardna greška proporcije:

$S E_{p} = \sqrt{\frac{p (1 - p)}{n}}$ gde je: $p$ , proporcija događaja u uzorku; $n$ broj opservacija.

Standardna greška aritmetičke sredine

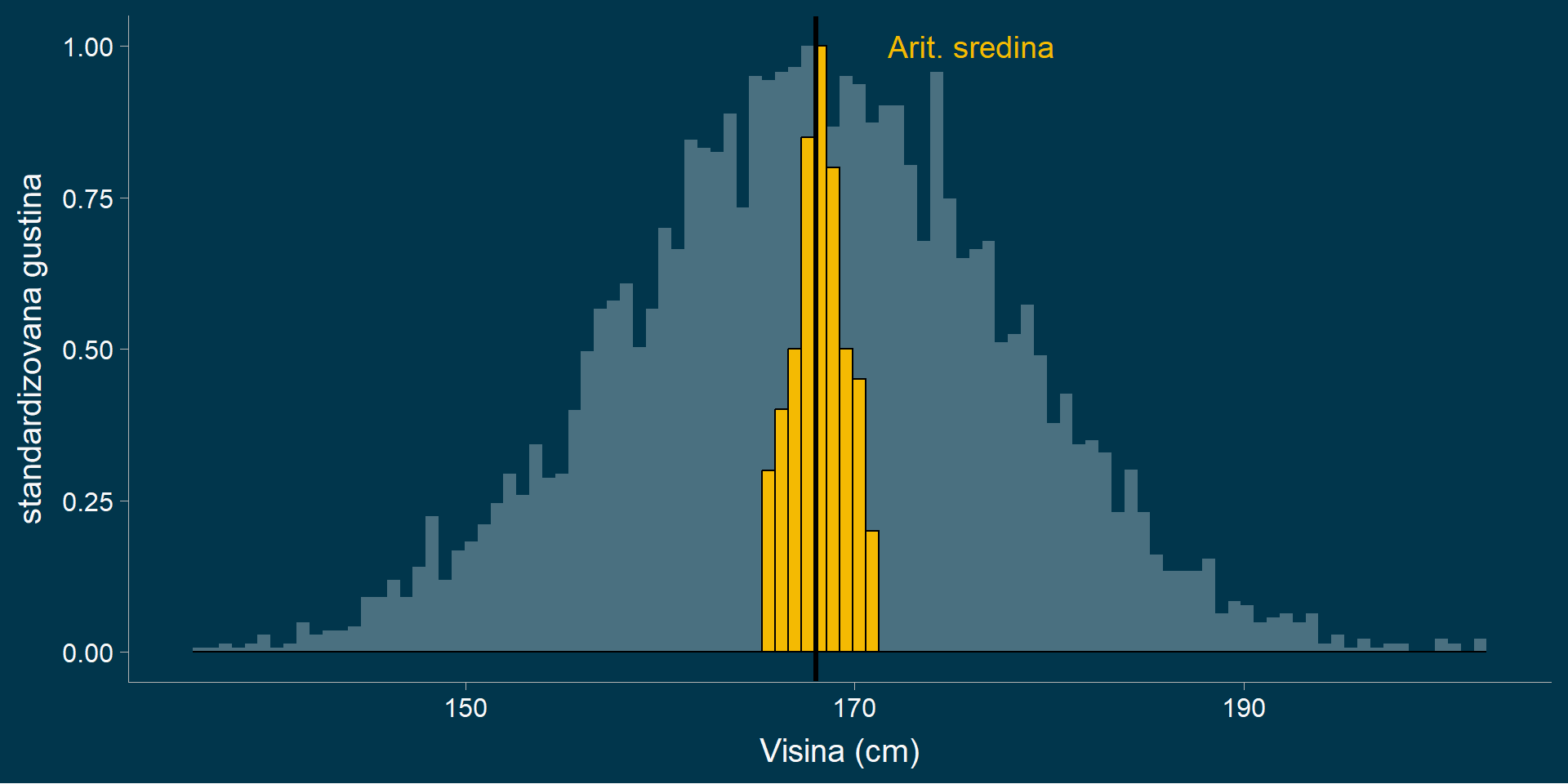
Primer centralne granične teoreme

Bilo koja raspodela $\to$ arit. sred. uzorka $\to$ normalna raspodela arit. sredina

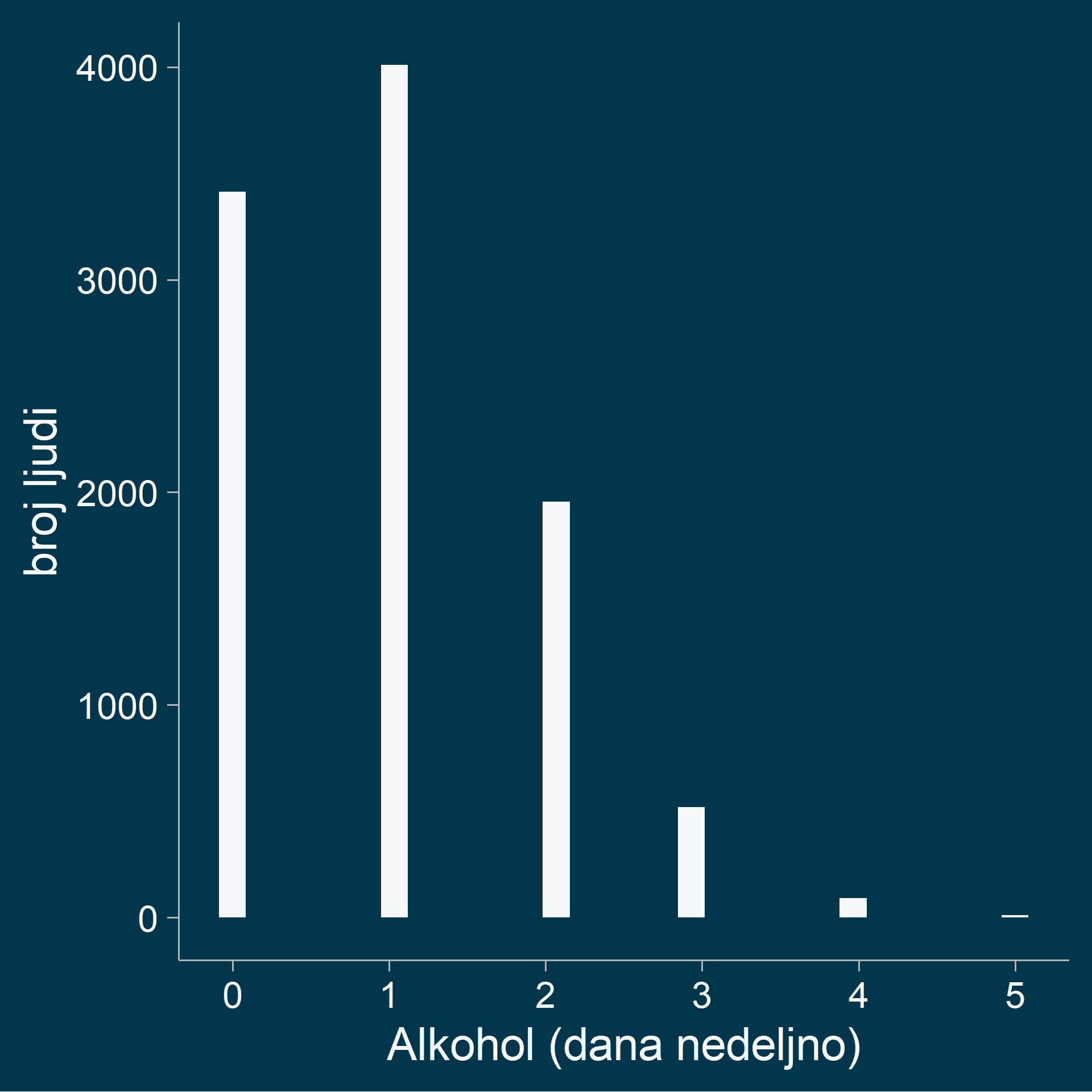
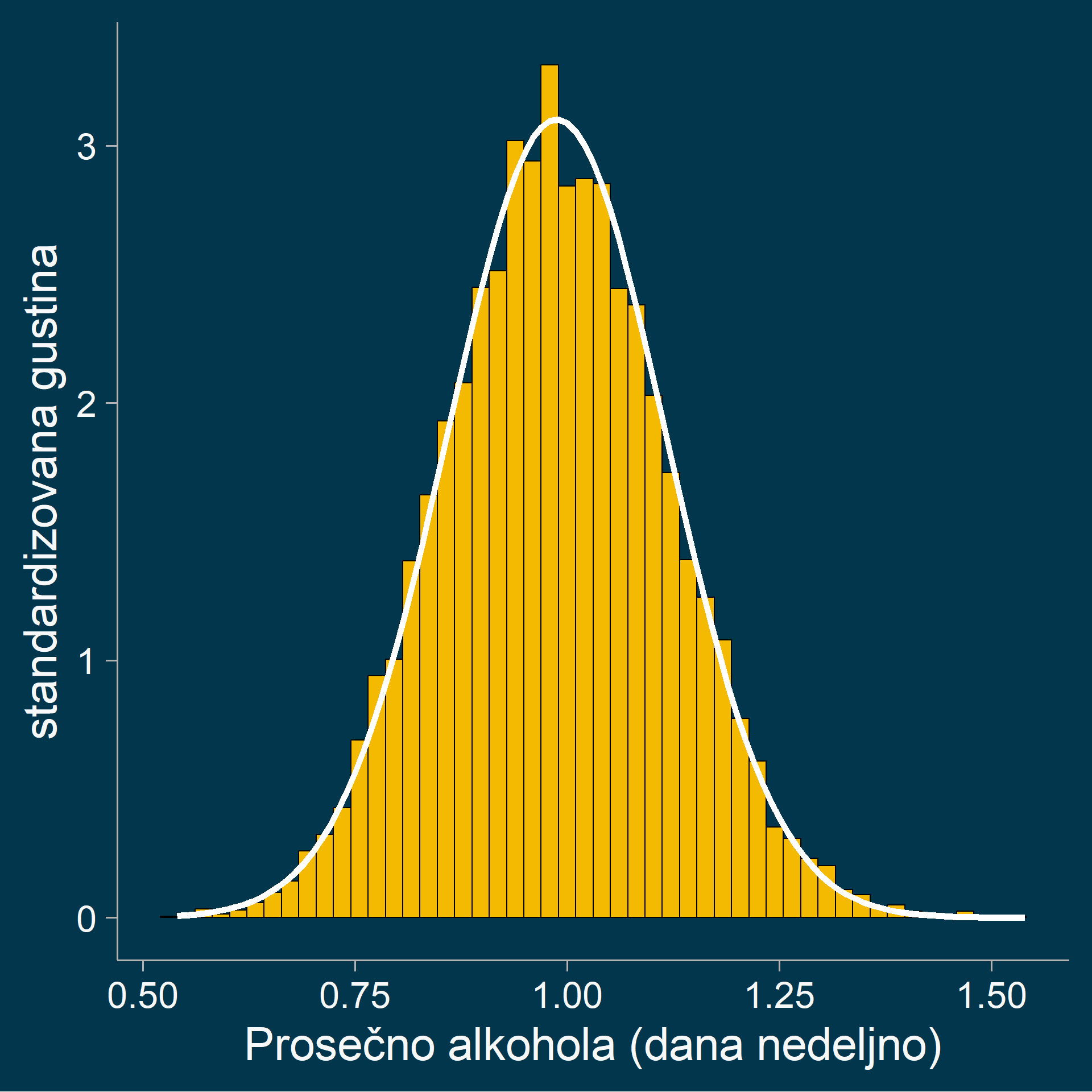
Ocenjivanje populacionih parametara na osnovu uzorka

Jedan od najvažnijih istraživačkih zadataka jeste ocena populacionih parametara, najčešće aritmetičke sredine ili proporcije.

Interval poverenja i tačkasta procena

$C I = \bar{x} \pm t \times S E$

gde je: $\bar{x}$ , aritmetička sredina; $t$ , kritična vrednost; $S E$ , standardna greška.

95% interval poverenja

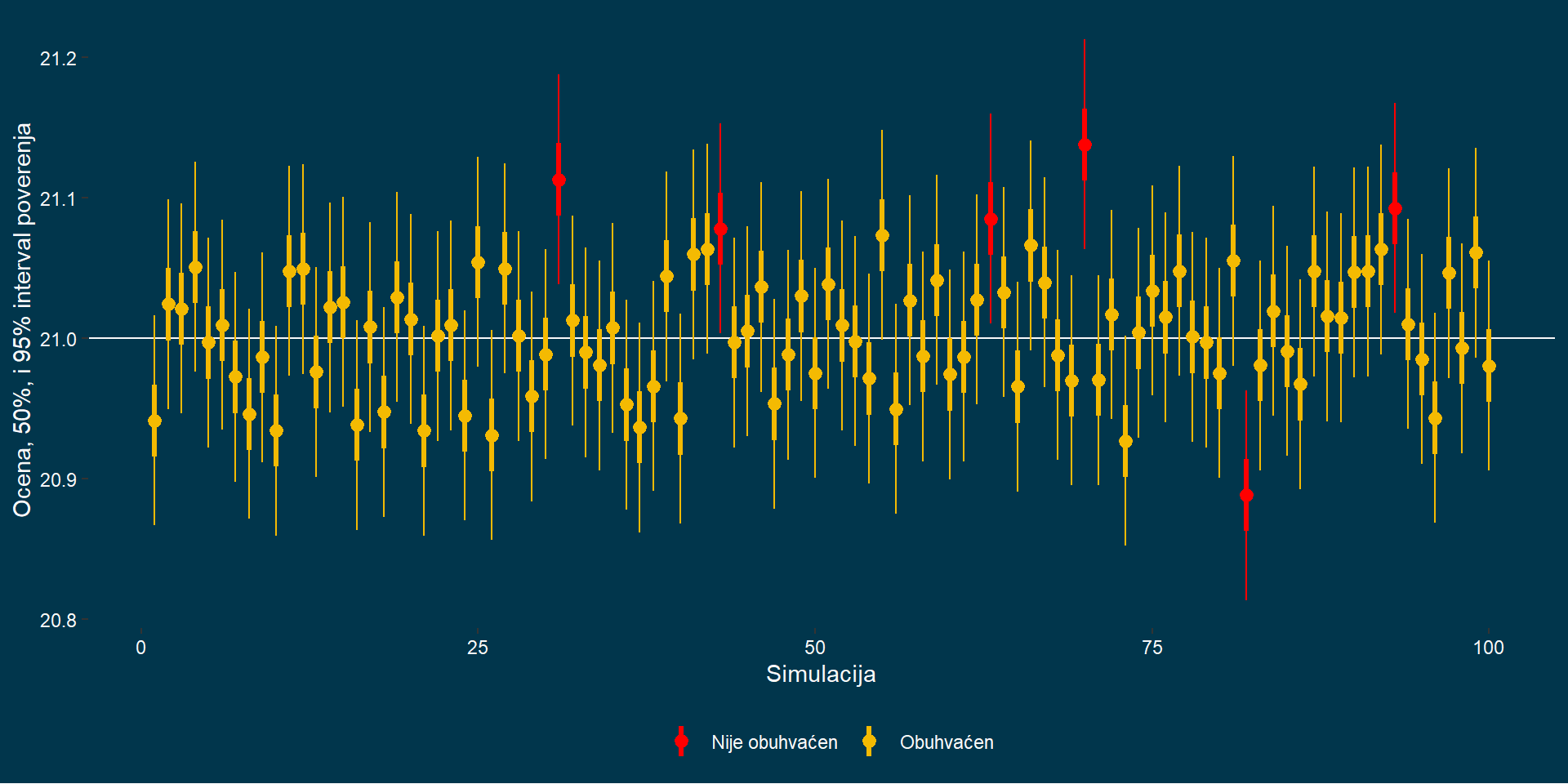
99% Inverval poverenja

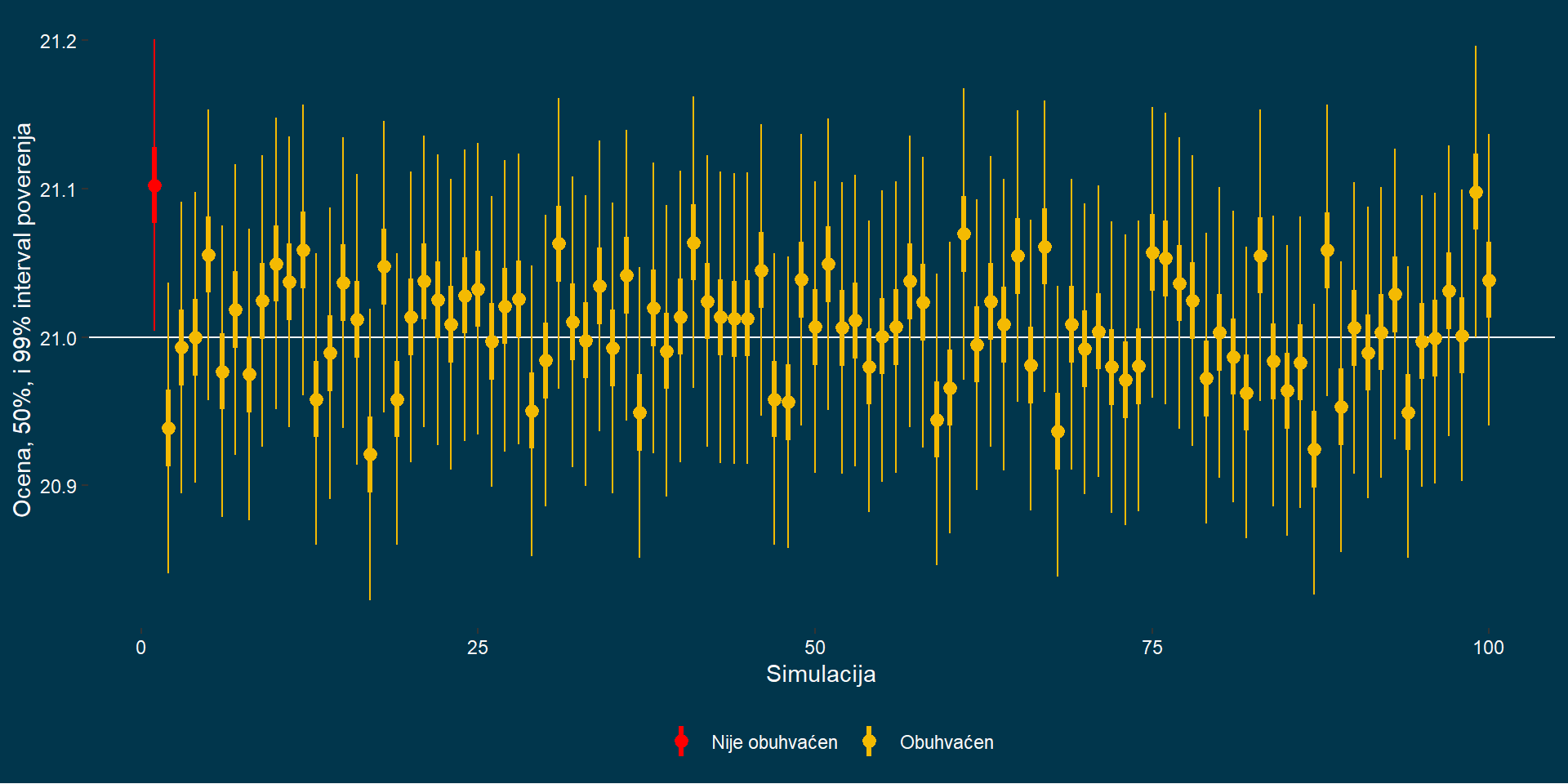
Definicija

Od svih 95% intervala poverenja, 95%

njih sadrži pravu populacionu vrednost.

95% vs. 99%

99% interval je sigurniji (ima manji

rizik greške) ali je širi od 95%.

Generalizacija

Saznanje o celoj populaciji bez da smo ih videli.

tinytable_u2089o5pdku3mq3sxdjm

Intervencija	Mortalitet	Ukupno	Stopa smrtnosti (%)	95% IP (%)
Agresivna terapija	92	439	21.0	17.24 - 25.07
Manje agresivna terapija	81	446	18.2	14.69 - 22.06

Vežba: interval poverenja za kontinuirane podatke

Koristeći bazu podataka Sistolna TA.xlsx odrediti

99% interval poverenja aritmetičke sredine

sistolnog arterijskog pritiska ispitanika sa

akutnim koronarnim sindromom.

Komande

Statistical analysis $\to$ Continuous variables $\to$ Single-sample t-test

Vežba: interval poverenja za diskretne podatke

Na uzorku od 500 učenika u jednoj opštini nađena je

anemija kod 25 učenika. Odrediti 95% interval

poverenja proporcije učenika sa anemijom u toj

opštini.

Komande

Statistical analysis $\to$ Discrete variables $\to$ Confidence interval for a proportion

Struktura kursa

tinytable_fovahntwldza2hpn0vv0

Nedelja	Tema
1	Uvod u medicinsku statistiku
2	Sređivanje podataka
3	Statističko opisivanje podataka
4	Verovatnoća i raspodele verovatnoća
5	Populacija i uzorak
6	Testiranje hipoteza o populacionim prosečnim vrednostima i proporcijama
7	Testiranje hipoteza o učestalostima
8	Testiranje hipoteza o rangovima
9	Korelacija
10	Regresija / Kolokvijum
11	Podaci, informacije i znanje
12	Zdravstveni informacioni sistem
13	Mere dijagnostičke tačnosti
14	Medicinsko odlučivanje
15	Bioinformatika

Populacija i uzorak