| Krvna grupa | Relativna učestalnost |
|---|---|
| O | 45% |
| А | 39% |
| B | 12% |
| AB | 4% |
Kratak uvod u verovatnoću
2024-10-31
de Méréov problem


Potreba za teorijom verovatnoće
Verovatnoća kao produžetak Aristotelove logike.
Dobijamo mogućnost da pričamo o (ne)sigurnosti ubeđenja.

Šta je verovatnoća
Eksperiment je aktivnost koja proizvodi ishod (biramo novi put da testiramo da li je brži od starog).
\[ \text{Eksperiment} \rightarrow \text{Ishod} \]
Prostor ishoda je skup svih mogućih ishoda eksperimenta.
\[ \text{Prostor ishoda kocke:} \; \omega = \{1,2,3,4,5,6\} \]
Događaj je podskup prostora ishoda.
\[ \text{Događaj bacanja kocke} \; x = 6 \]
Kako delimo događaje?
Događaj je skup mogućih ishoda, a može biti:
Deterministički (Nedostatak vitamina C \(\rightarrow\) Skorbut)
Slučajni (stohastnični)
Prostor (elementarnih) ishoda \(\omega\) je skup svih mogućih ishoda.
\[ \omega = \{A, B\, O, AB\} \; \; \; \omega = \{\text{zdrav}, \text{bolestan}\} \]
Somatske ili germinativne mutacije
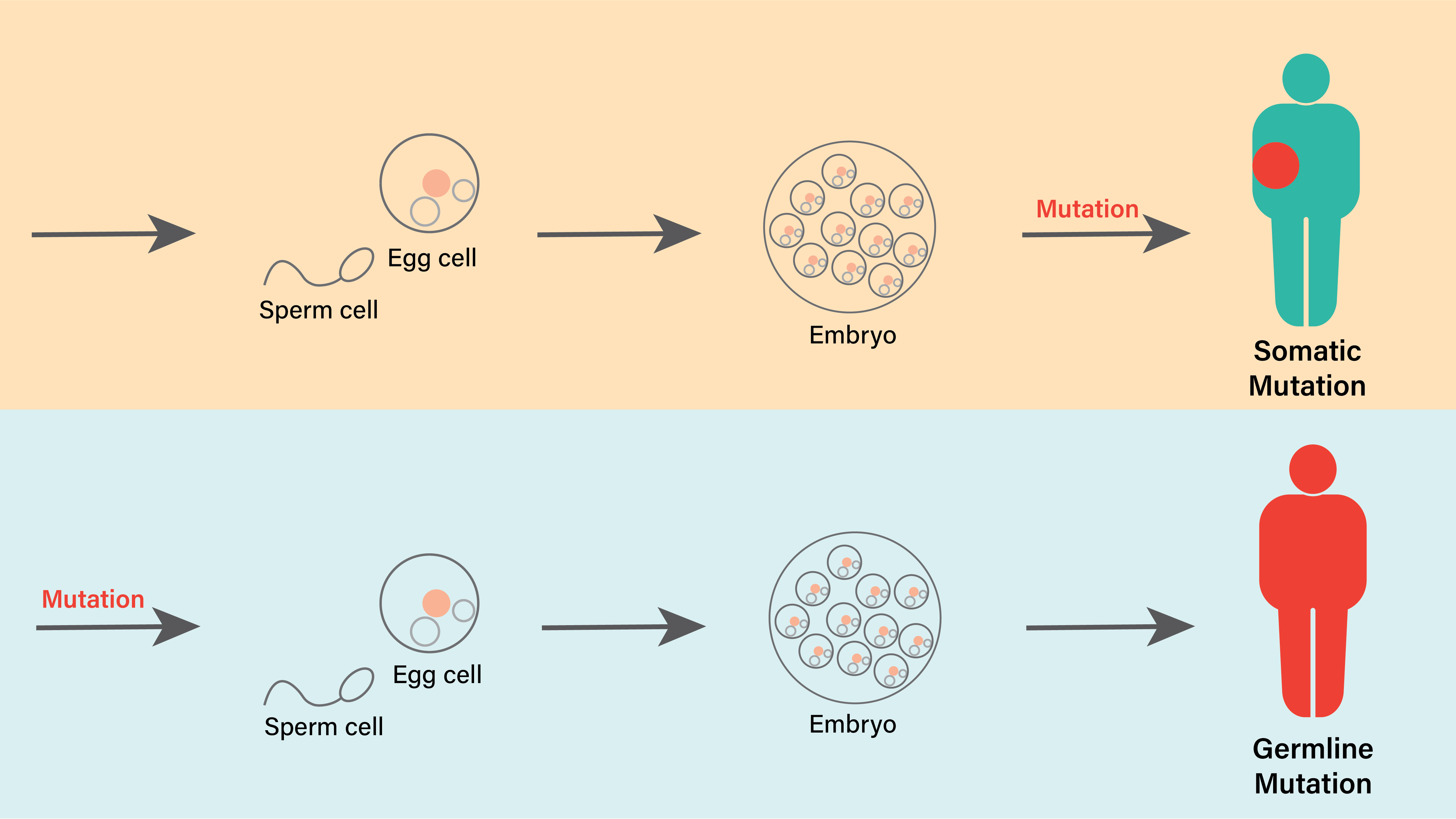
Definicija verovatnoće
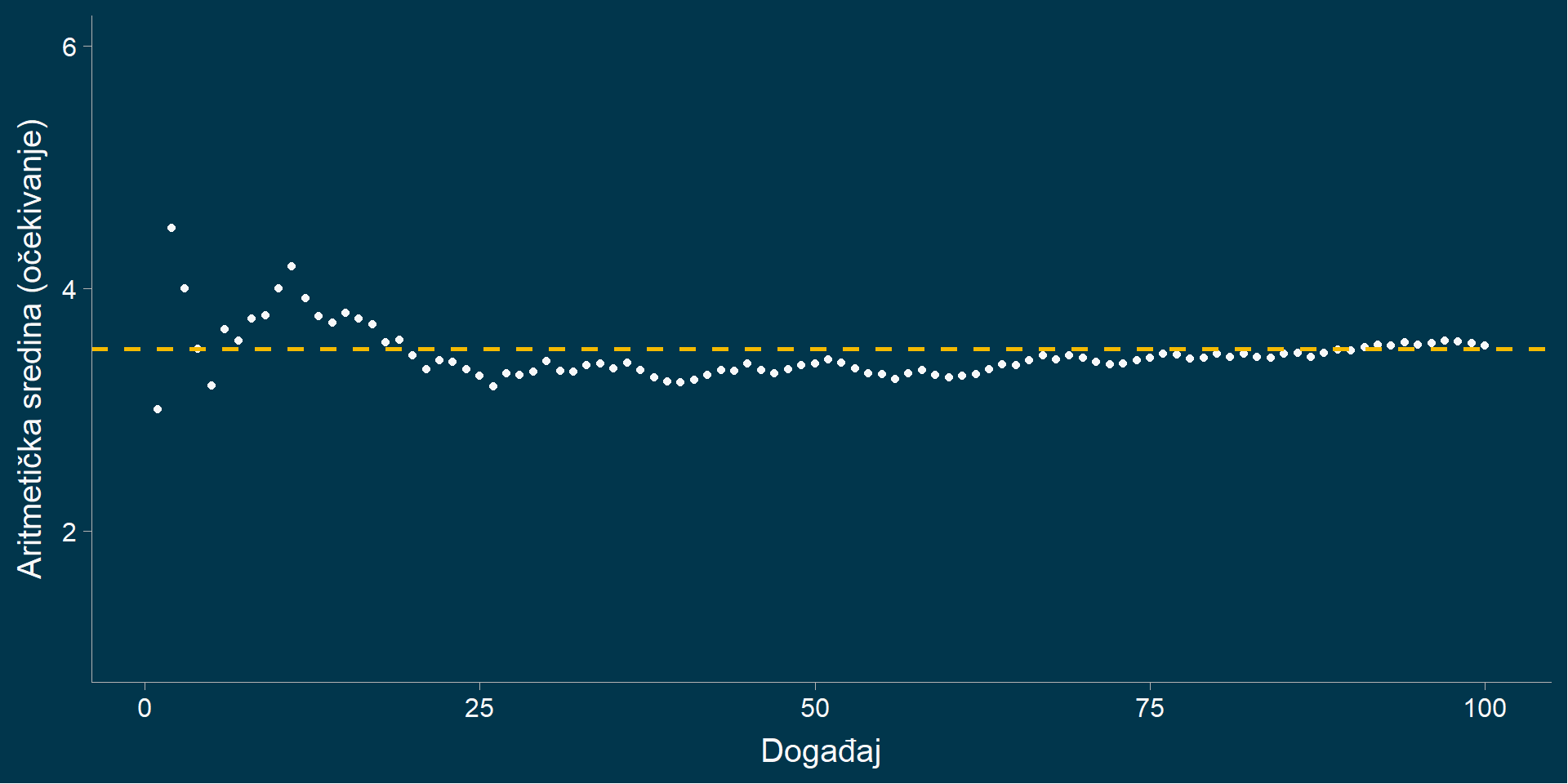
Verovatnoća je mera očekivanja
nekog slučajnog događaja.
Očekivanje je opštije od aritmetičke sredine

Beleška
Očekivanja su svuda u medicini: preživljavanje, vreme do oporavka nakon uzimanja leka, lab. testovi (markeri, biohem. parametri, eGFR), itd.
Zakon velikih brojeva
Kako određujemo verovatnoću?
- Objektivna
- Teorijska (matematička)
- Empirijska (statistička)
- Subjektivna
- Ubeđenje
Teorijska verovatnoća
- Znamo je pre merenja
- Svi mogući ishodi su jednako verovatni

Empirijska verovatnoća
Empirijska verovatnoća se određuje (brojanjem) posle posmatranog događaja.
\[ p = \frac{\text{očekivano}}{\text{ukupno}} \]
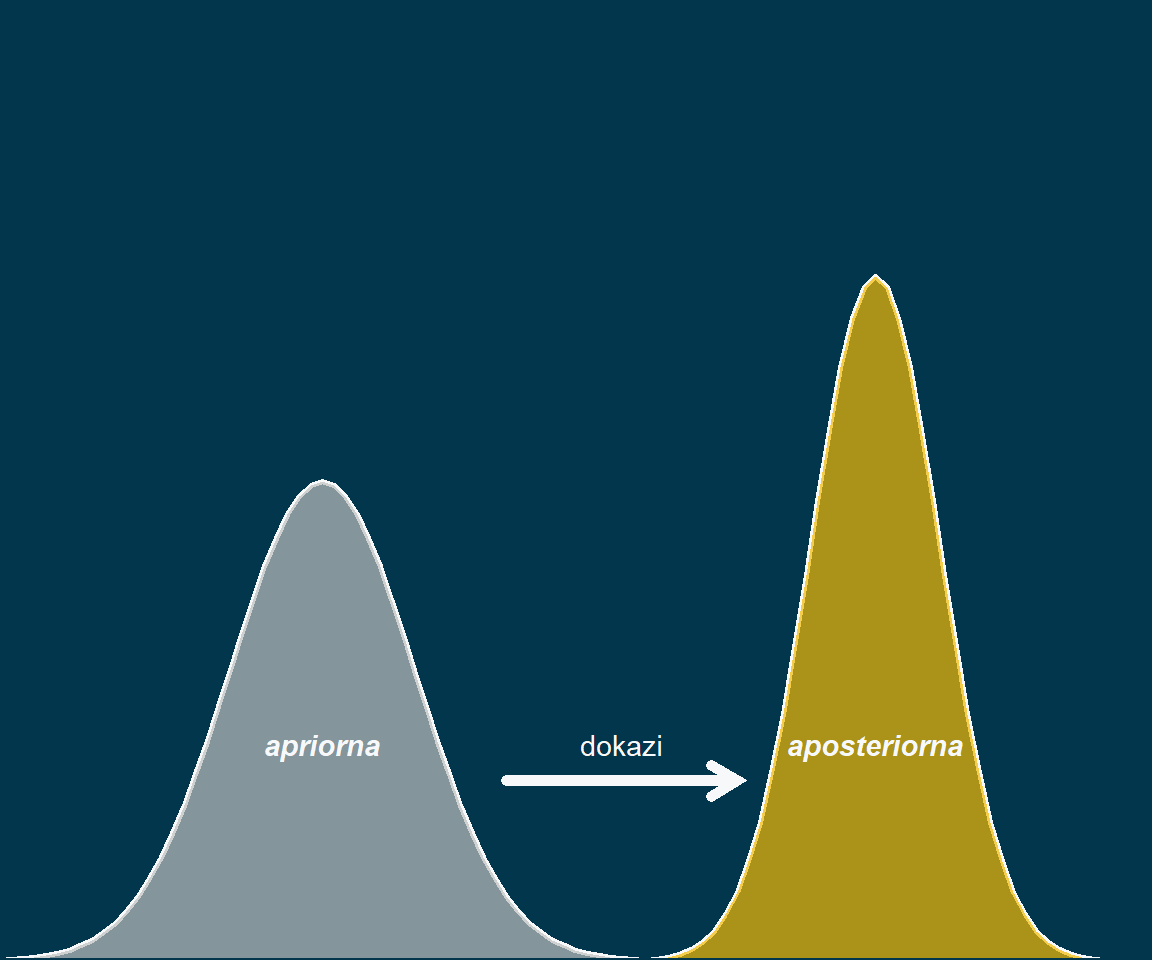
Subjektivna verovatnoća
- Uverenje
- Ekspertsko mišljenje
flowchart TD
S(Simptom) --> A("Apriorna Verovatnoća")
Z(Znak) --> A
P(Prevlenca) --> A
A --> T{"Dijagnostički test"}
T --> AP("Aposteriorna Verovatnoća")
Osobine verovatnoće
Aksiomi:
- Nenegativnost [0, 1]
- Normiranost (zbir = 1)
- Aditivnost
Dodatni termini:
- Verovatnoća događaja (\(p\))
- Verovatnoća suprotnog događaja (\(1-p = q\))
- Komplementarnost (\(p+q = 1\))
Isključivost
Događaji su isključivi ako ne mogu da se dogode istovremeno.
- Krvna grupa
- Prisustvo simptoma gripa
- Prisustvo medicinskog znaka
- Dijagnoze
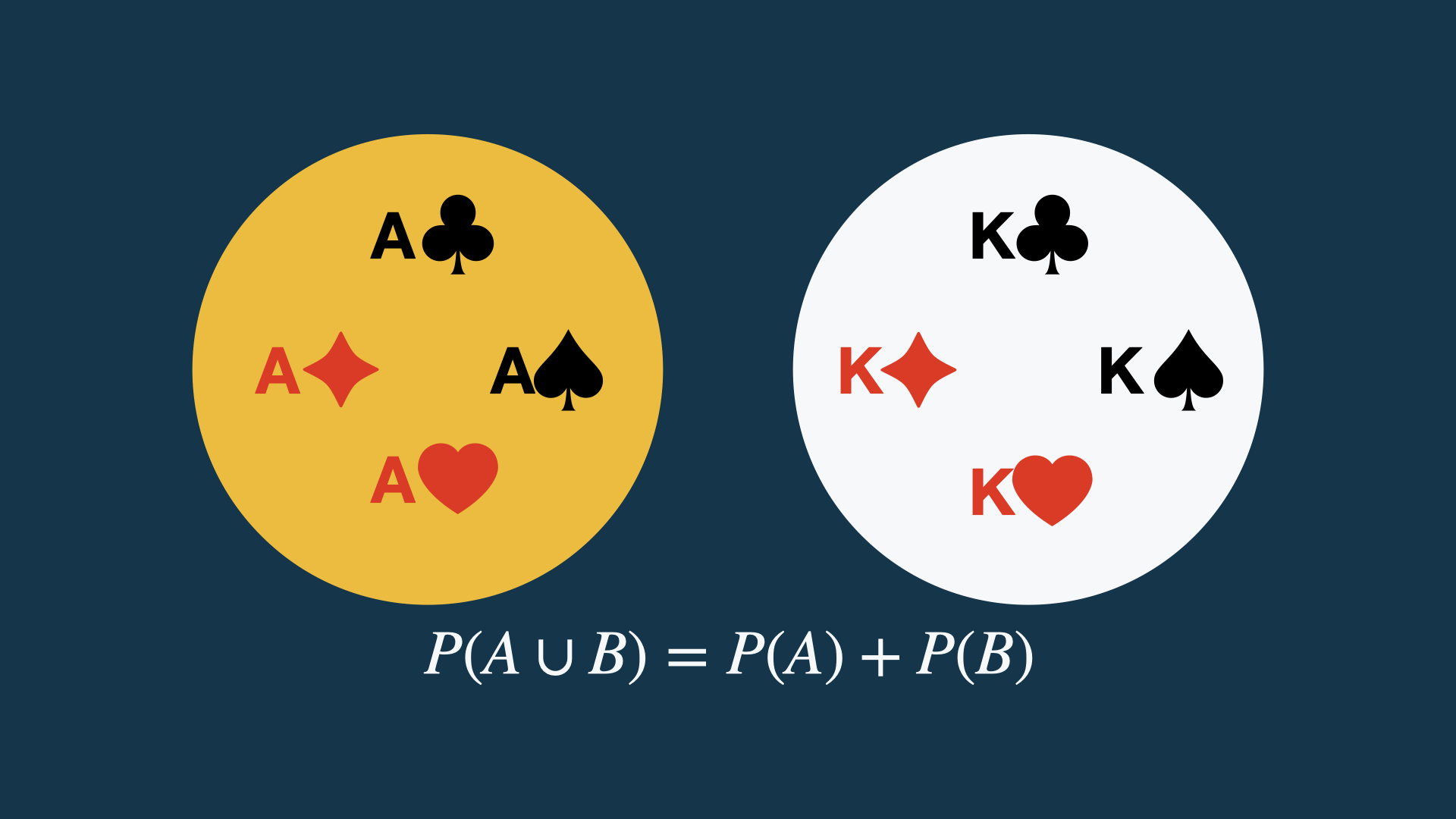
Zakoni verovatnoće: adicija (1)
Adicija (sabiranje verovatnoća) isključivih događaja.
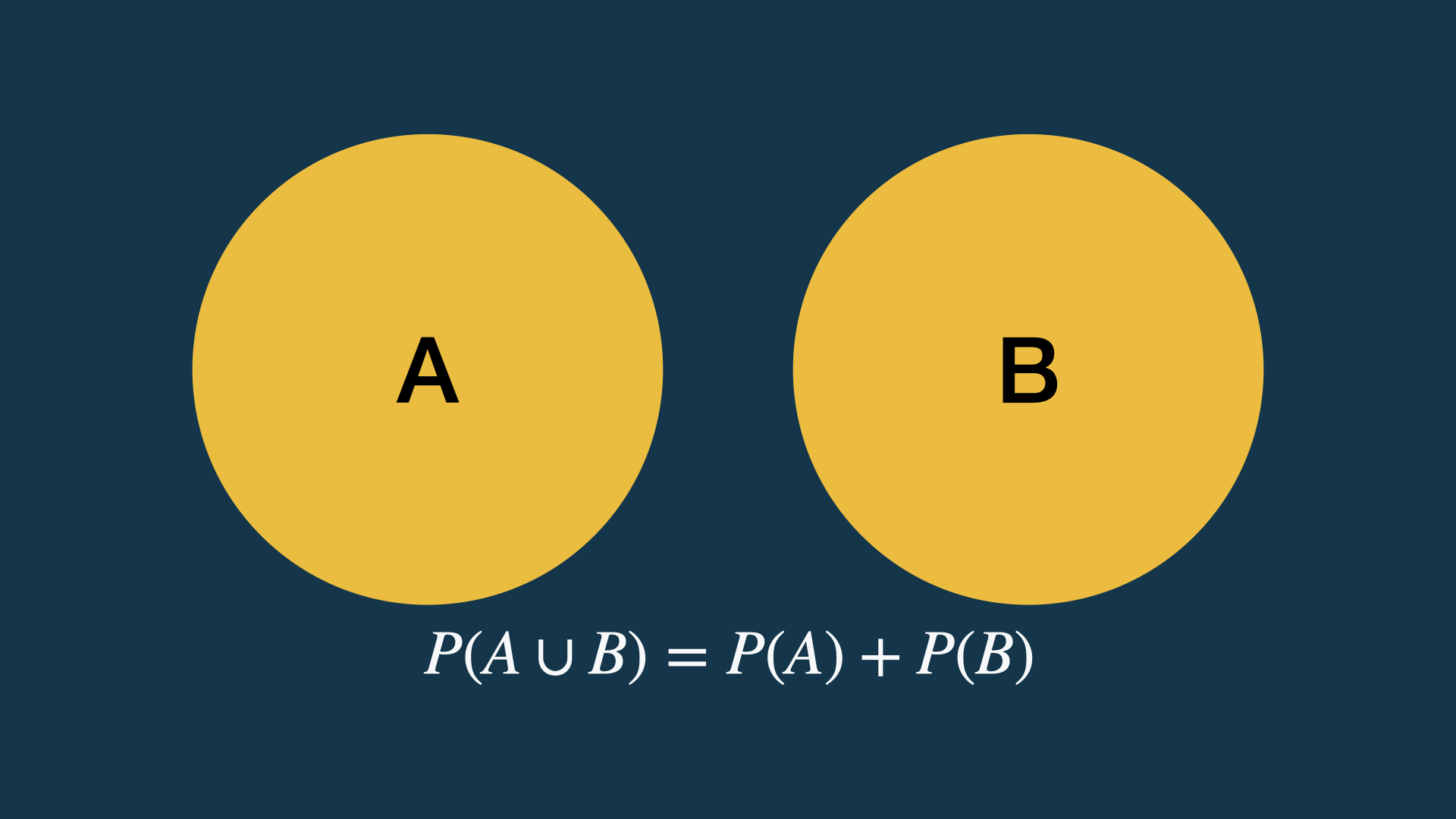
Zakoni verovatnoće: adicija (2)
Adicija (sabiranje verovatnoća) neisključivih događaja.
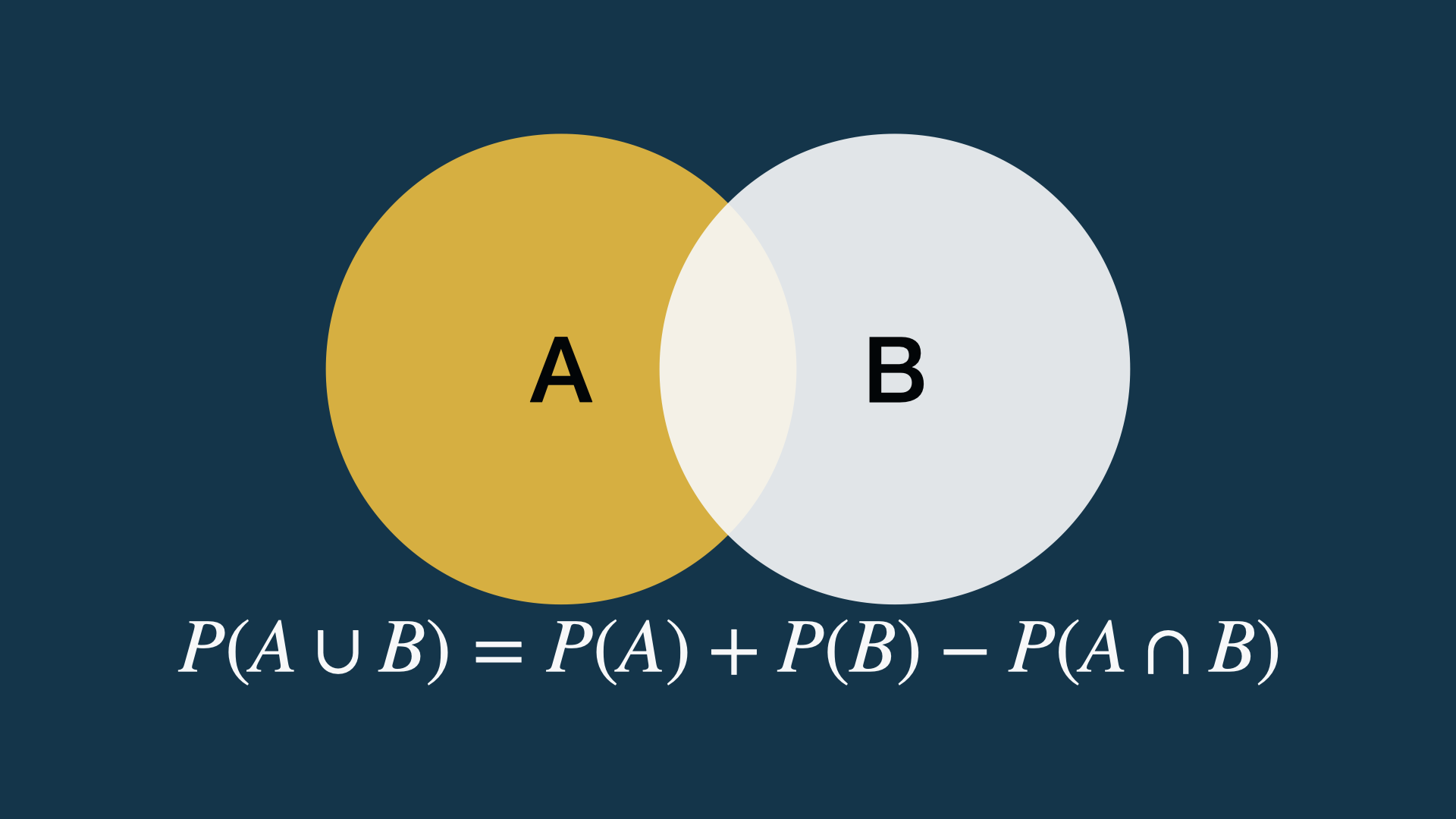
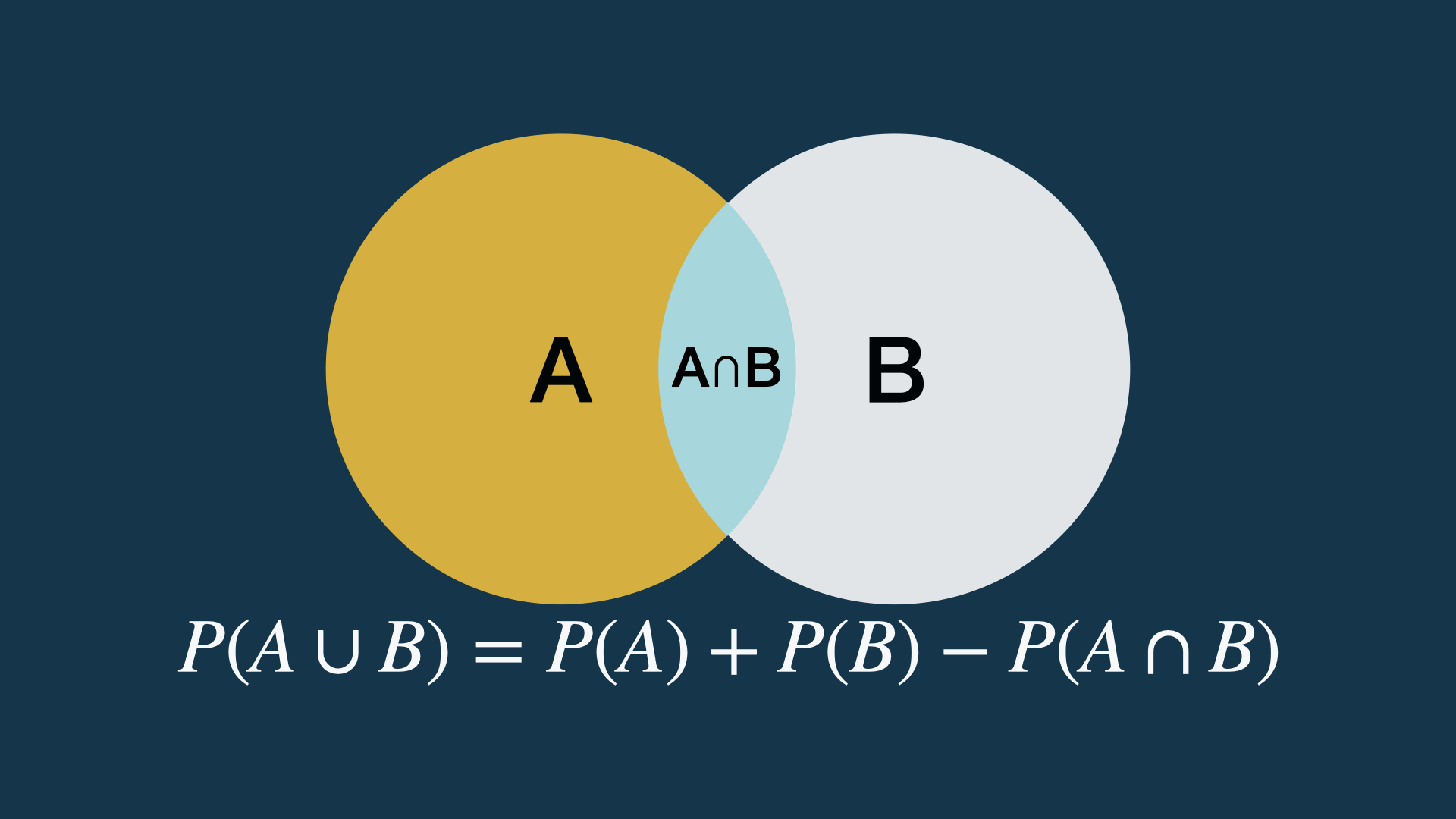
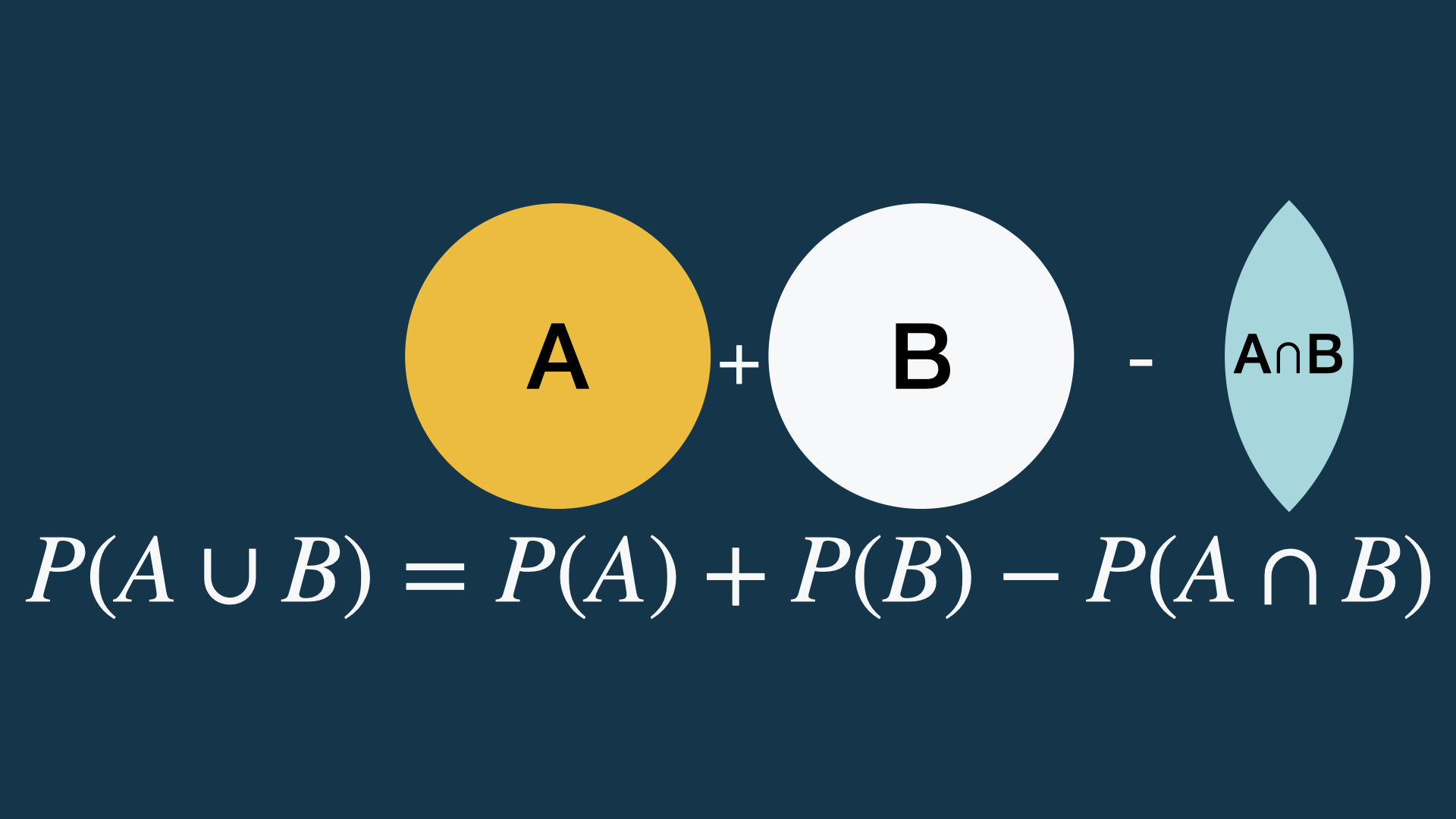
Zakoni verovatnoće: multiplikacija
Multiplikacija isključivih događaja.
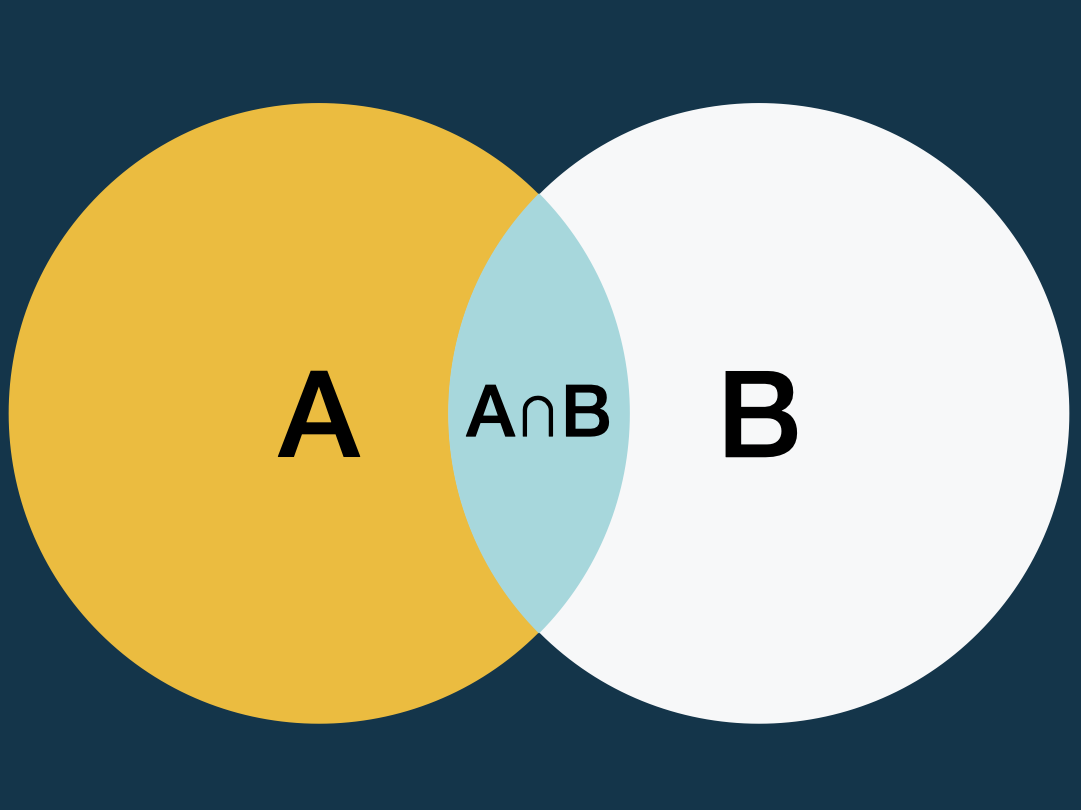
\[ P(A \cap B) = P(A) \times P(B) \]
Verovatnoća zavisnih (uslovnih) događaja

\[ P(A \cap B) = P(A) \times P(B|A) = P(B) \times P(A|B) \]
Verovatnoća u dijagnostici

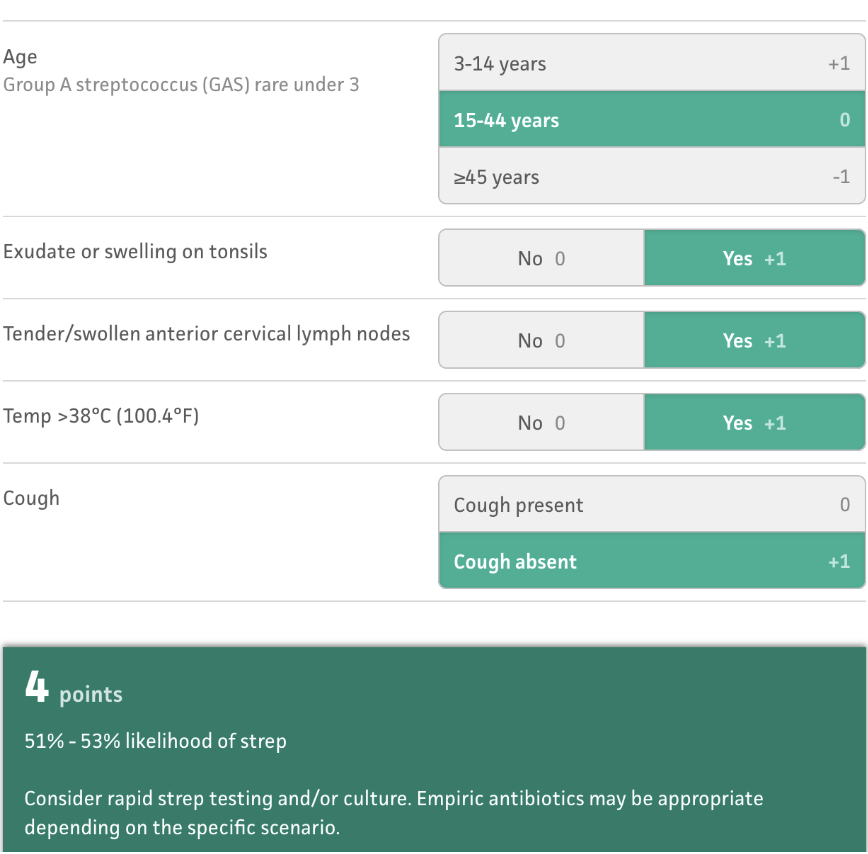
CENTOR Skor
- Doprinos svakog simptoma/znaka verovatnoći strep. infekcije
- Rezultat je pre-test verovatnoca
Teorijske raspodele verovatnoća
Teorijske raspodele verovatnoća su specifični matematički opisi (modeli) slučajnih događaja.
- Binomna
- Normalna
Metematički model


Bernulijev eksperiment
Binomna raspodela
Uslovi:
- Isključivi događaji
- Konstantna verovatnoća
- Nezavisni
Binomna verovatnoća je data:
\[ P(X = x) = \frac{n!}{x!(n-x)!}p^{x}q^{n-x} \]
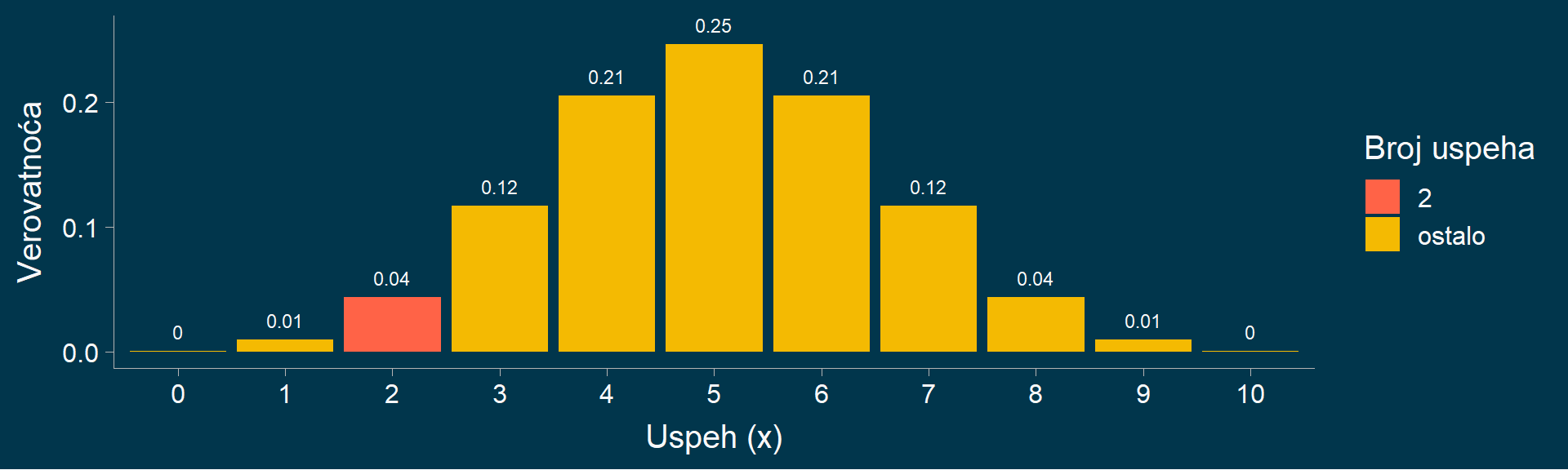
Zadatak 1
Učestalost hipertenzije u populaciji starijih od 65 godina iznosi 42%.
Kolika je verovatnoća da u slučajnom uzorku veličine 7 osoba,
izabranom iz te iste populacije, dve osobe imaju hipertenziju?
Zašto je normalna distribucija česta?
- Normlana distrubucija nastaje sabiranjem (ili množenjem) rezultata mnogo sitnijih procesa.
- Na primer, greške u merenju, varijacije rasta, i brzina molekula su procesi u kojima se javlja.

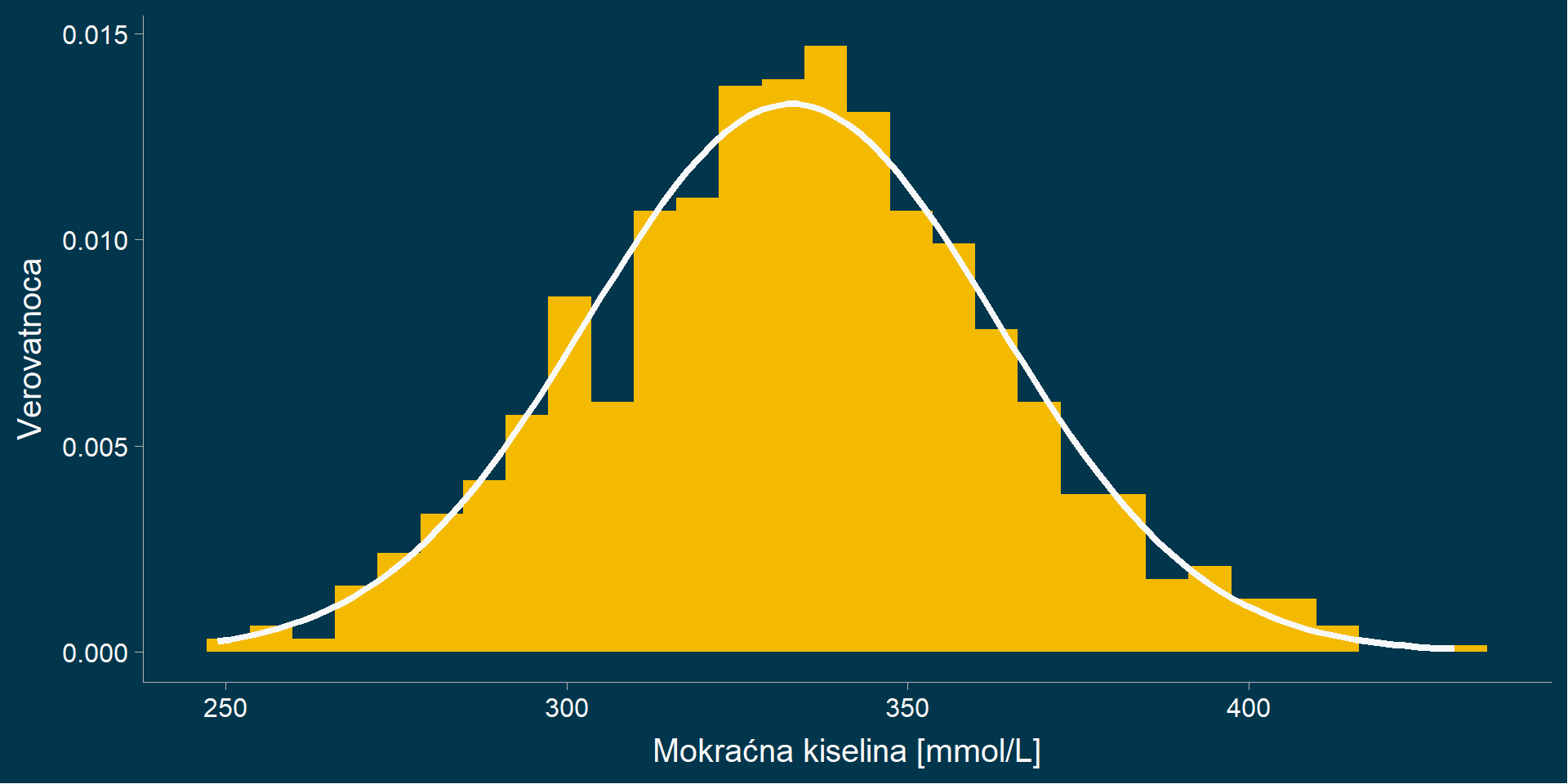
Normalna raspodela
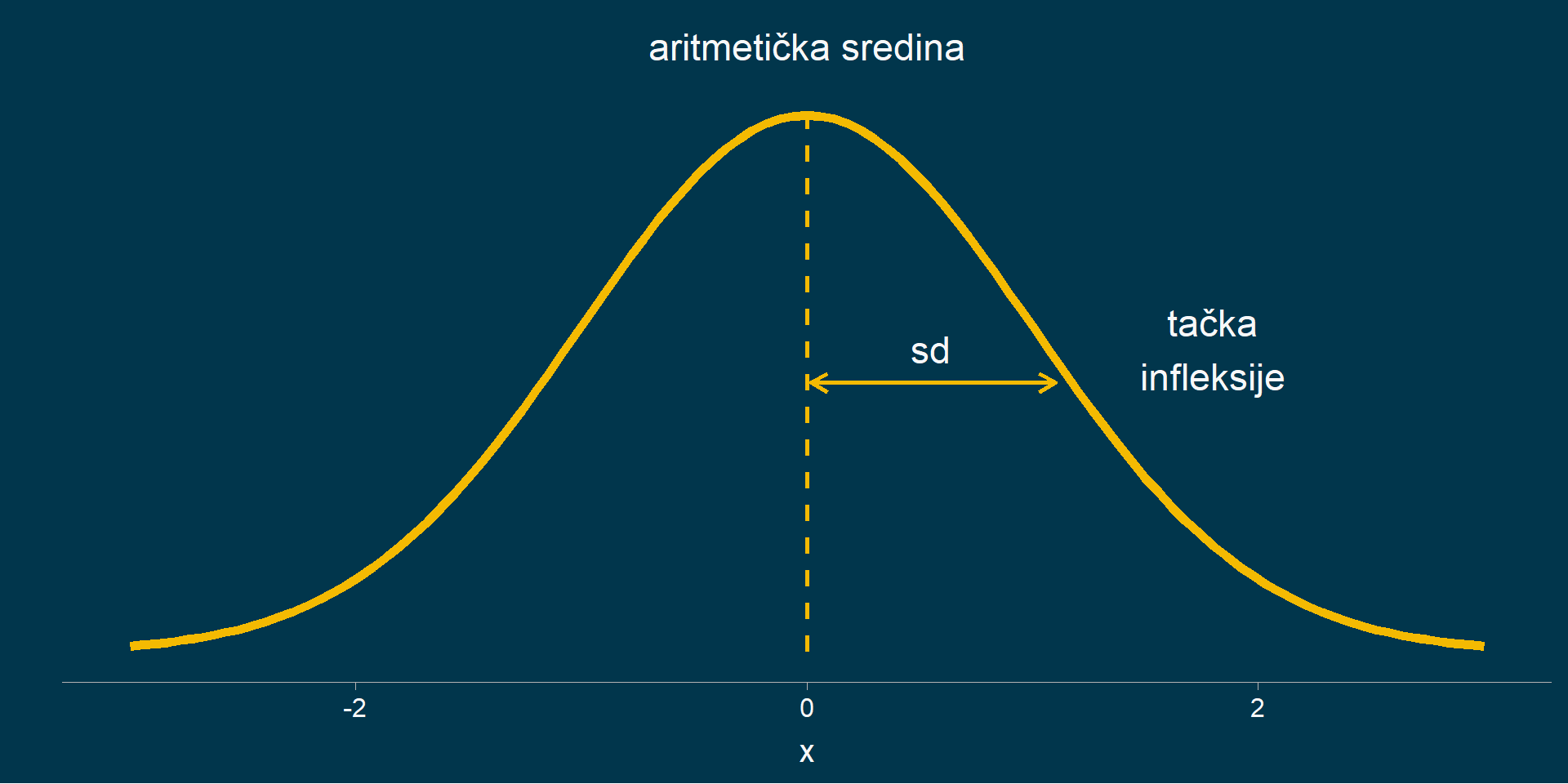
Standardna normalna reaspodela
Normalna raspodela gde je \(\bar x = 0\) i \(sd = 1\). Dobija se formulom:
\[ z_i = \frac{x_i - \mu}{\sigma} \]
Nekada bila bitna zbog tablica verovatnoca.
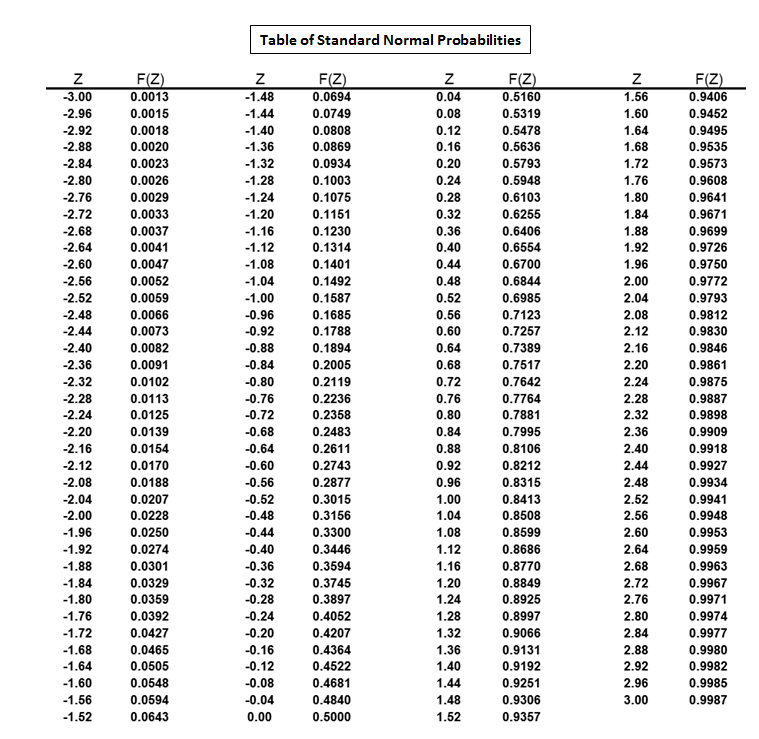
Tablica verovatnoća
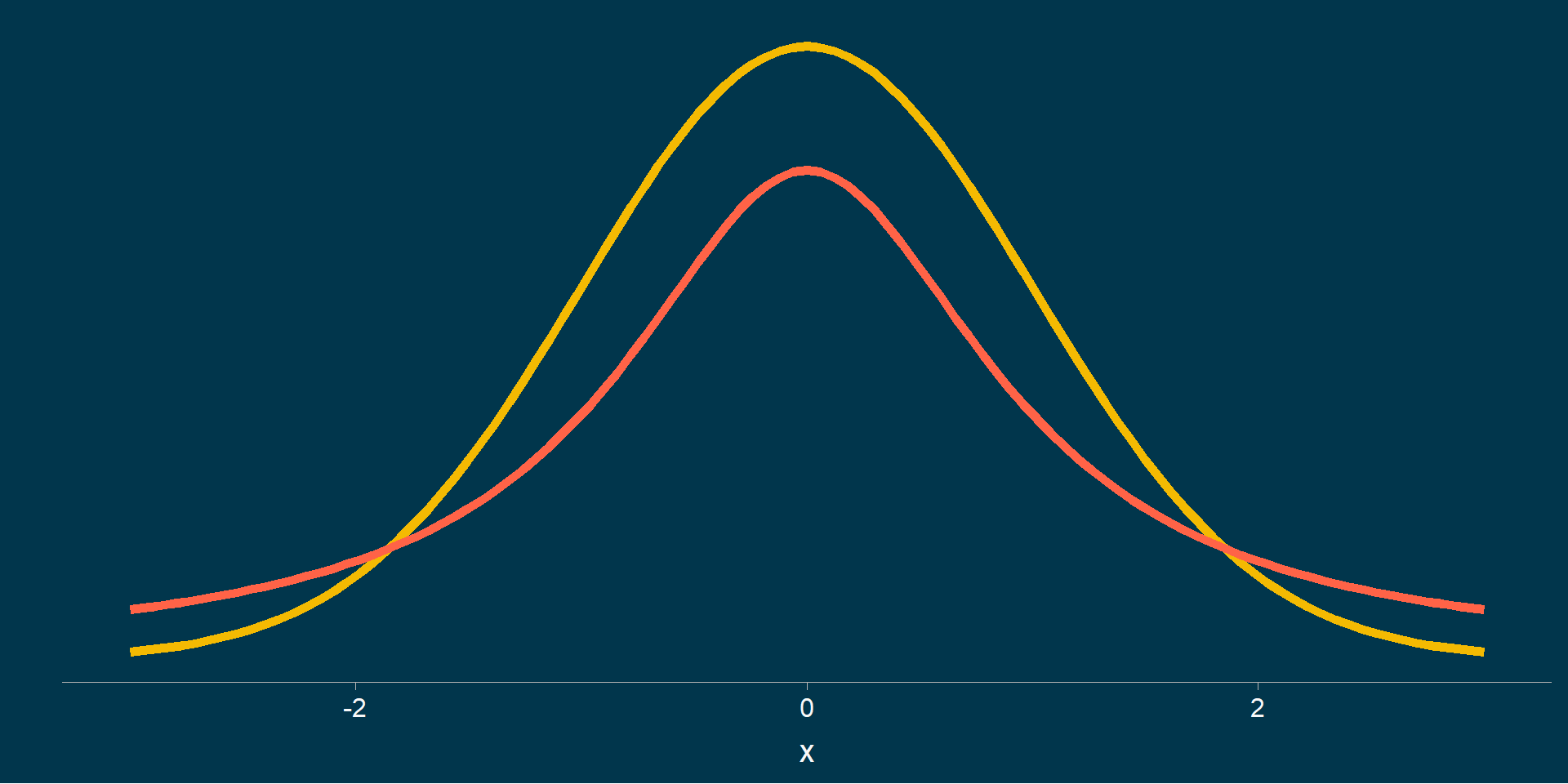
Studentova t-distribucija
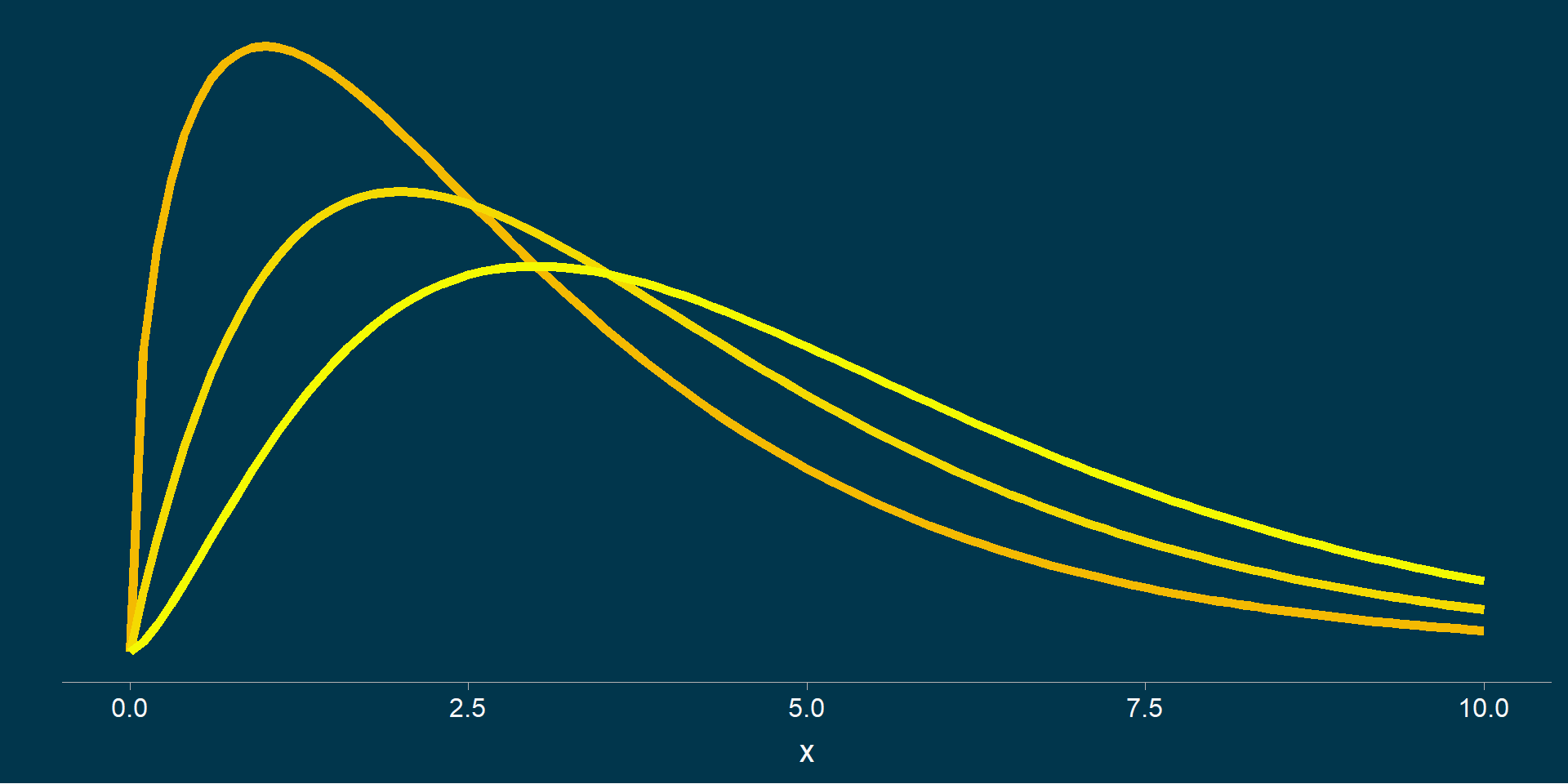
Hi-kvadratna distribucija
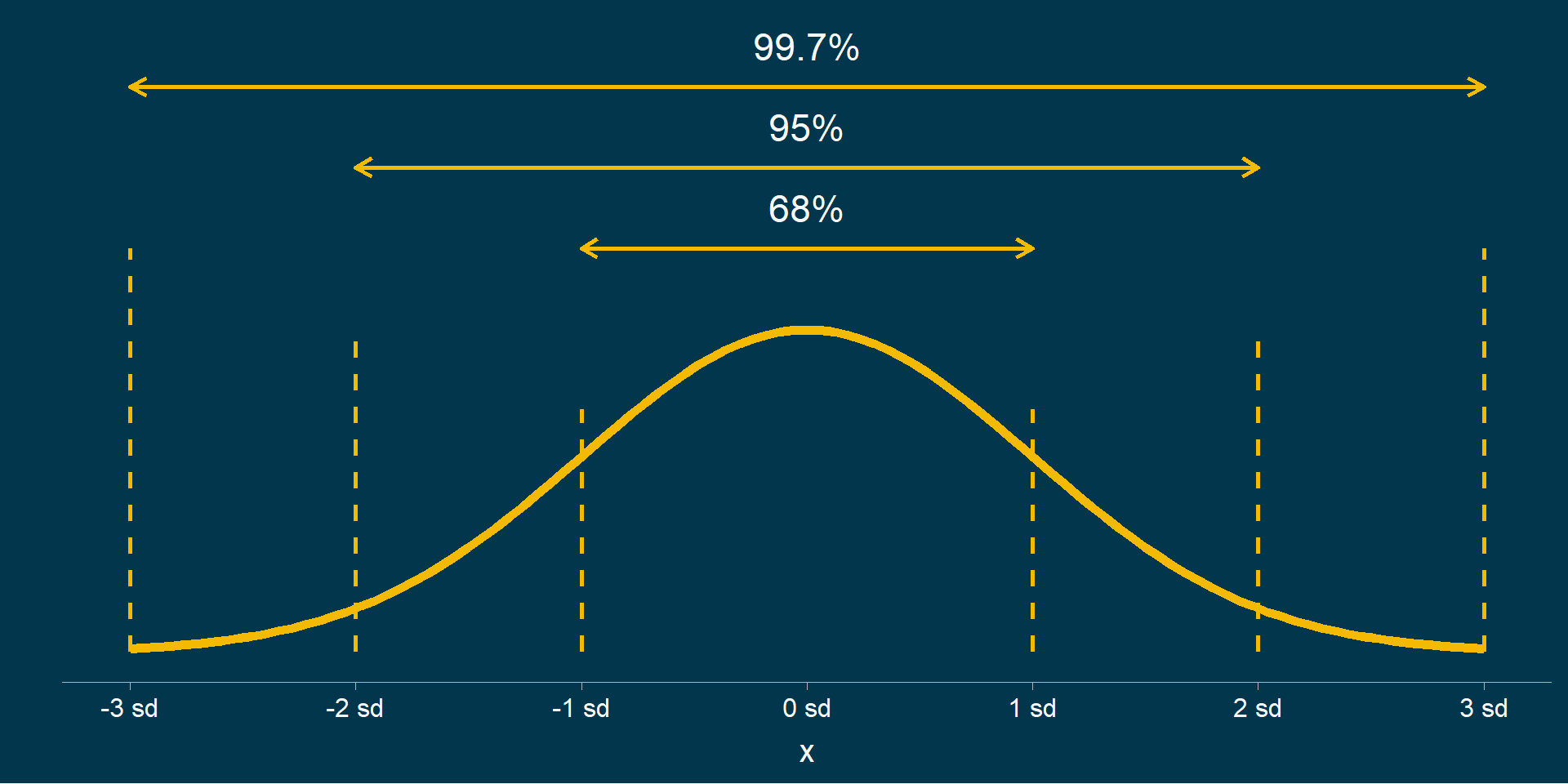
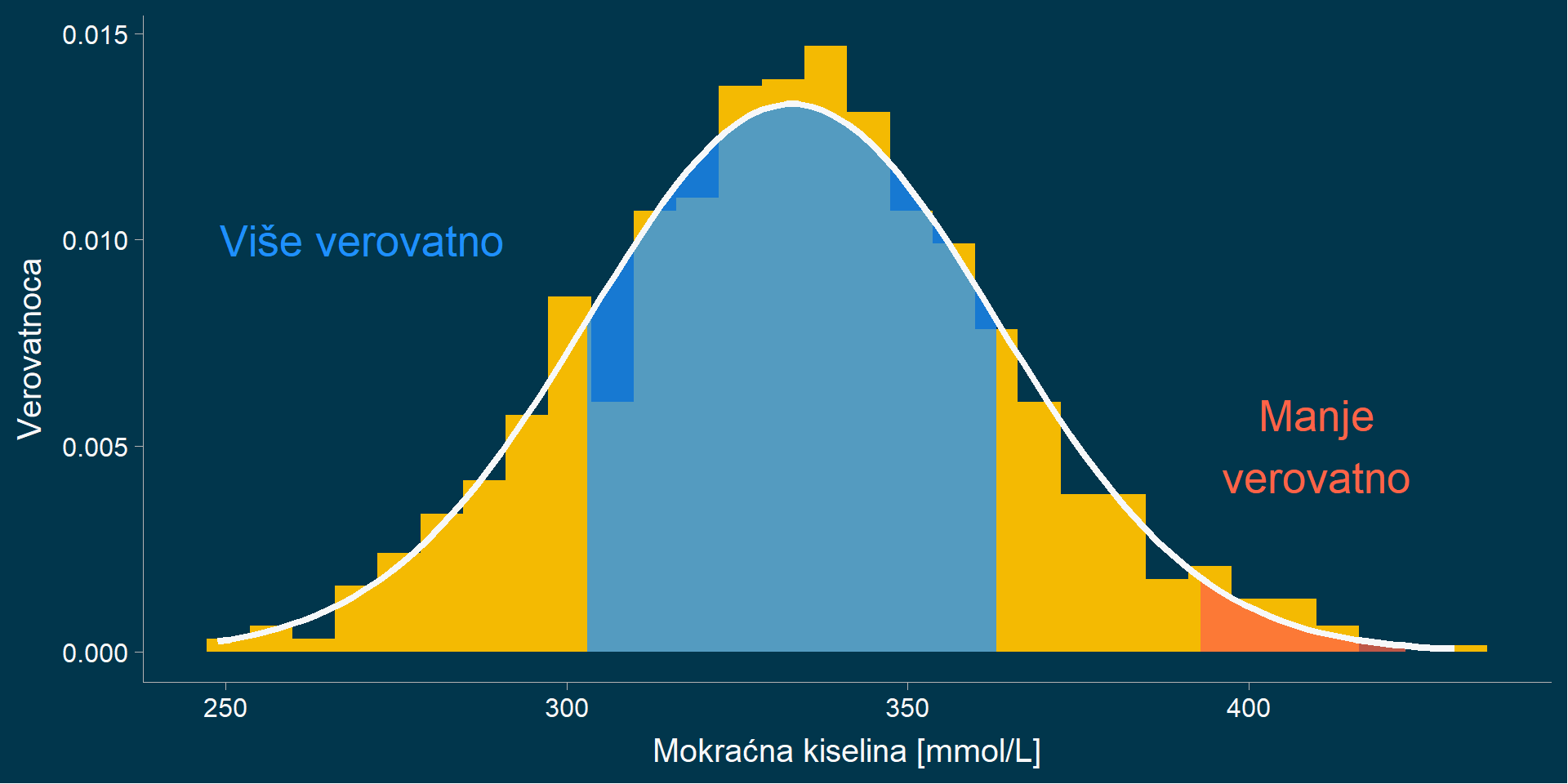
68-95-99.7
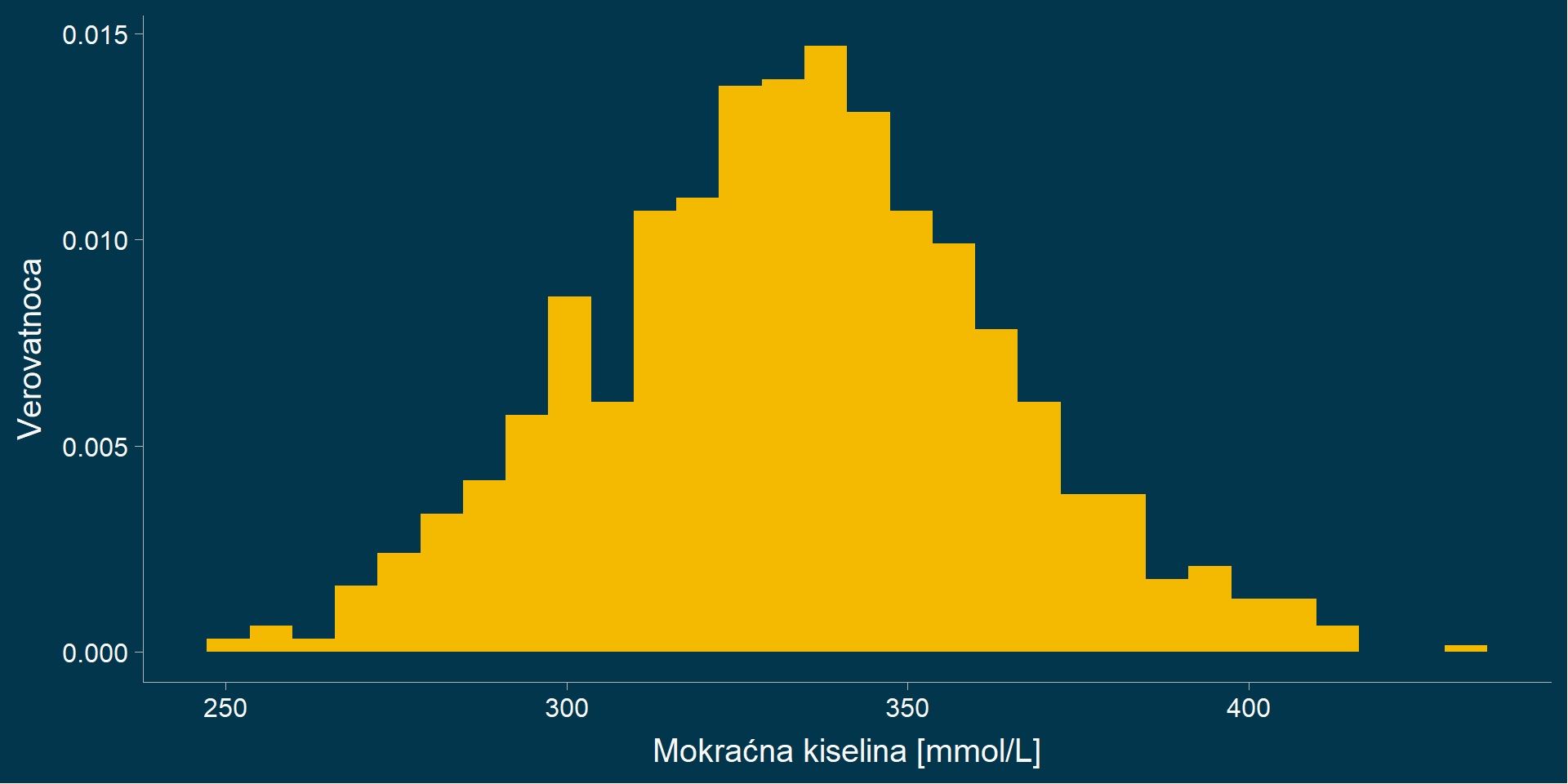
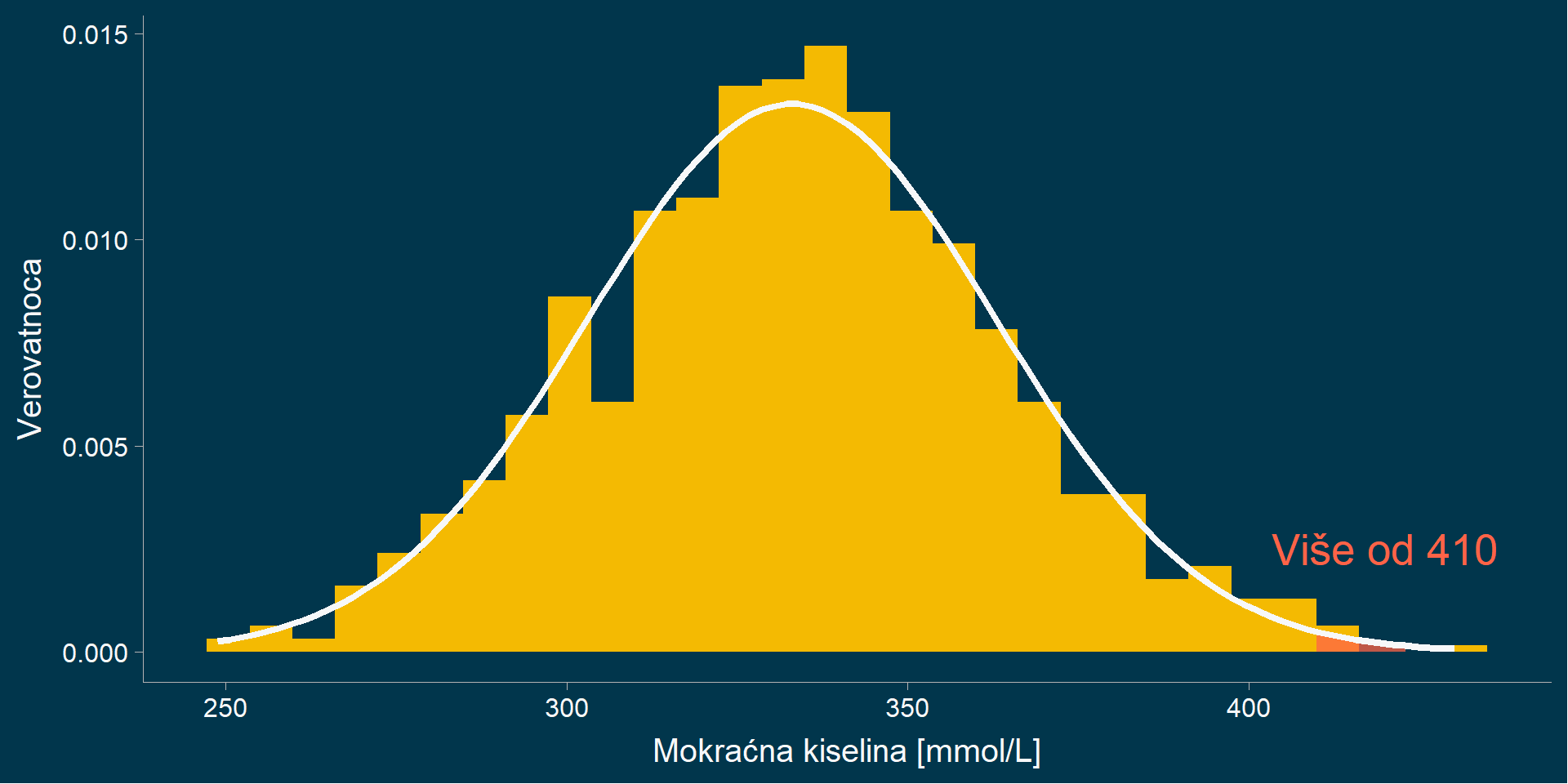
Zadatak 2
U populaciji žena starosti između 25 i 50 godina vrednosti mokraćne kiseline u
serumu su normalno raspoređene sa aritmetičkom sredinom 333 mmol/L i
standardnom devijacijom 30 mmol/L.
Kolika je verovatnoća da slučajno izabrana osoba iz ove populacije ima
vrednost mokraćne kiseline u serumu veću od 410 mmol/l?
Računanje verovatnoće: normalna raspodela
Struktura kursa
| Nedelja | Tema |
|---|---|
| 1 | Uvod u medicinsku statistiku |
| 2 | Sređivanje podataka |
| 3 | Statističko opisivanje podataka |
| 4 | Verovatnoća i raspodele verovatnoća |
| 5 | Populacija i uzorak |
| 6 | Testiranje hipoteza o populacionim prosečnim vrednostima i proporcijama |
| 7 | Testiranje hipoteza o učestalostima |
| 8 | Testiranje hipoteza o rangovima |
| 9 | Korelacija |
| 10 | Regresija / Kolokvijum |
| 11 | Podaci, informacije i znanje |
| 12 | Zdravstveni informacioni sistem |
| 13 | Mere dijagnostičke tačnosti |
| 14 | Medicinsko odlučivanje |
| 15 | Bioinformatika |

