A short introduction to probability

Dr Nikola Grubor

2024-10-31

de Méré’s problem

Pierre de Fermat

Blaise Pascal

The need for probability theory

Probability as an extension of Aristotle’s logic.

We get to talk about the (un)certainty of belief.

Basic terms in probability theory

Experiment

An activity that produces an outcome (choosing a new path to test if it is faster than the old one).

\[ \text{Experiment} \rightarrow \text{Outcome} \]

Sample space

The set of all possible outcomes of an experiment.

\[ \text{Dice sample space:} \; \omega = \{1,2,3,4,5,6\} \]

Event

A subset of the outcome space.

\[ \text{Dice roll event} \; x = 6 \]

Types of events

An event is a set of possible outcomes, and can be:

• Deterministic (e.g. Vitamin C deficiency \(\rightarrow\) Scurvy)

• Random (stochastic)

The sample space of (elementary) outcomes \(\omega\) is a set of all possible outcomes.

\[ \omega = \{A, B\, O, AB\} \; \; \; \omega = \{\text{healthy}, \text{sick}\} \]

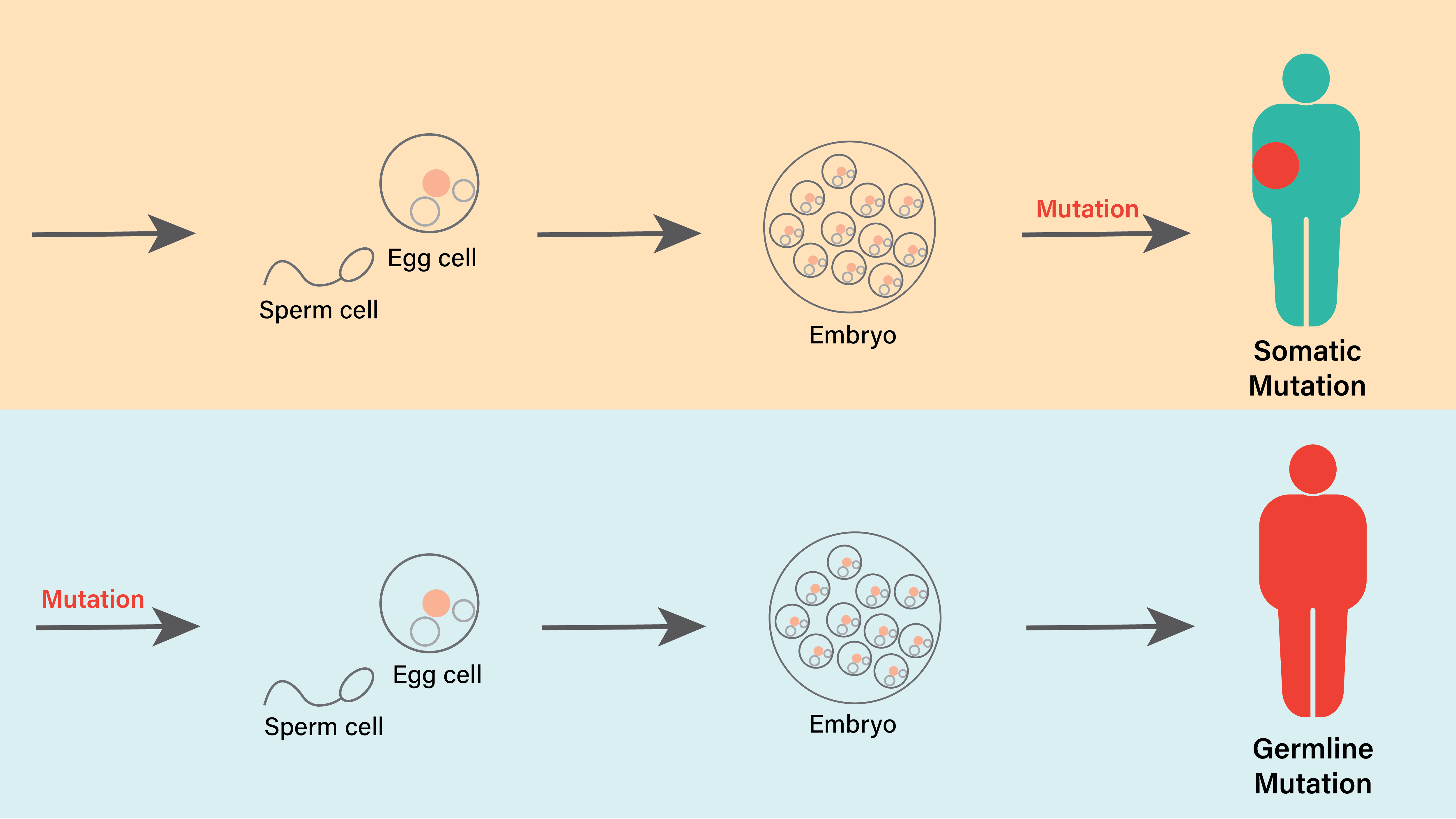
Somatic or germline mutations

Definition of probability

Probability is a measure of expectation

of some random event.

A random event = the result of a process that we don’t know how it works. Measure, process by which I add a number to something (meter and distance, knowledge and grades).

Expectation is more general than the mean

Note

Expectations are everywhere in medicine: survival, time to recovery after taking the drug, lab. tests (markers, biochemical parameters, eGFR), etc.

The expected value does not have to be the most common (mode), nor does it does have to coincide with everyday use. It doesn’t even have to be a value that can happen to be 3.5 on a 6-sided die.

Law of large numbers

How do we determine probability?

1. Objective
   • Theoretical (mathematical)
   • Empirical (statistical)
2. Subjective
   • Belief

Theoretical probability

• Available before measurement
• All possible outcomes are equally likely

Empirical probability

Empirical probability is determined (by counting) after observing the event.

\[ p = \frac{\text{expected}}{\text{total}} \]

Blood group	Relative frequency
O	45%
A	39%
B	12%
AB	4%

Subjective probability

• Belief
• Expert opinion

flowchart TD
  S(Symptom) --> A("Prior Belief")
  Z(Sign) --> A
  P(Prevalence) --> A
  A --> T{"Diagnostic test"}
  T --> AP("Posterior Belief")

Properties of probability

Axioms:

• Non-negativity [0, 1]
• Normality (sum = 1)
• Additivity

Additional dates:

• Event probability (\(p\))
• Probability of the opposite event (\(1-p = q\))
• Complementarity (\(p+q = 1\))

Exclusivity

Events are exclusive if they cannot occur simultaneously.

• Blood group
• Flu symptoms
• Medical sign
• Diagnoses

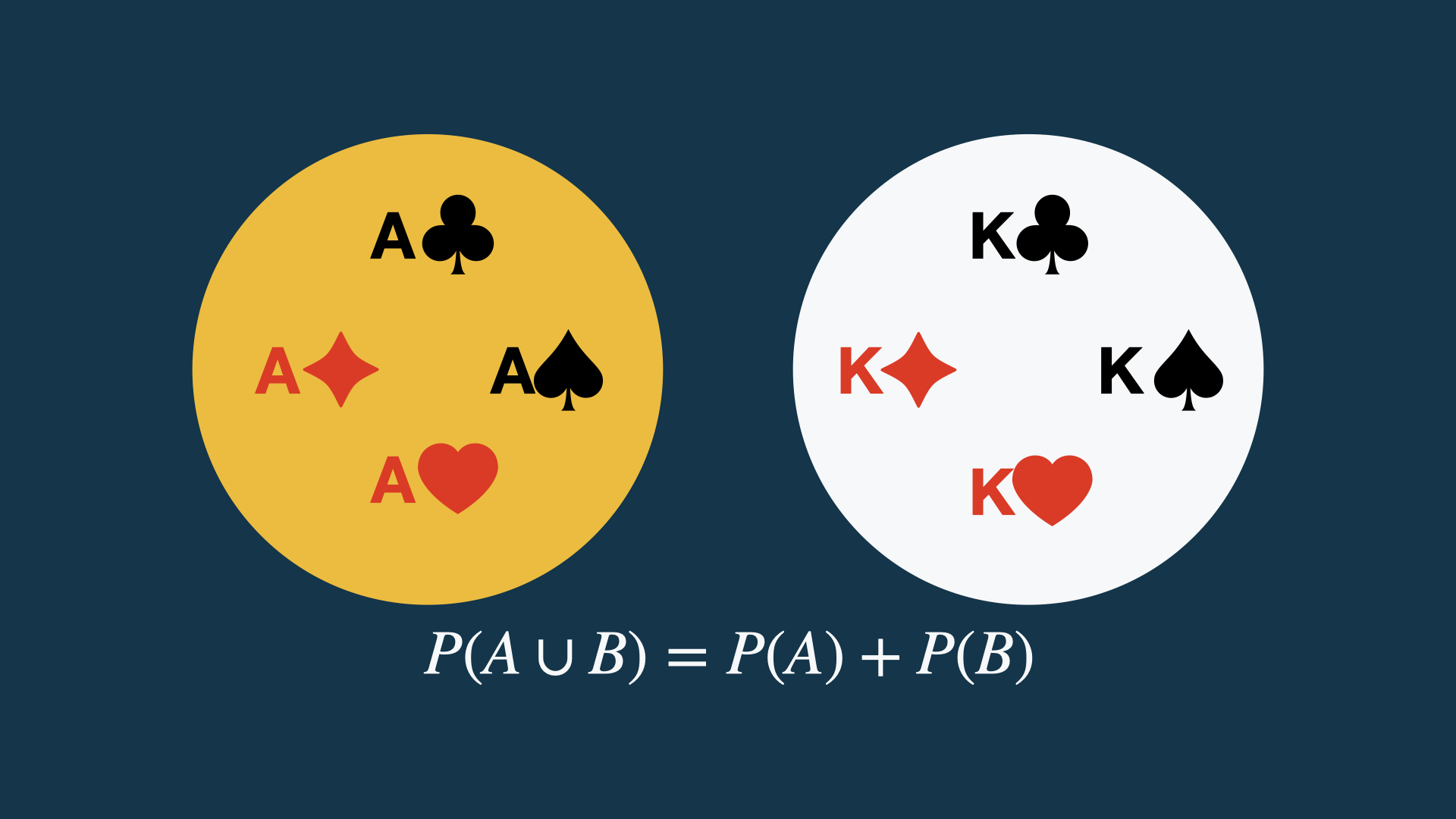
Laws of probability: addition (1)

Addition (summation of probabilities) of exclusive events.

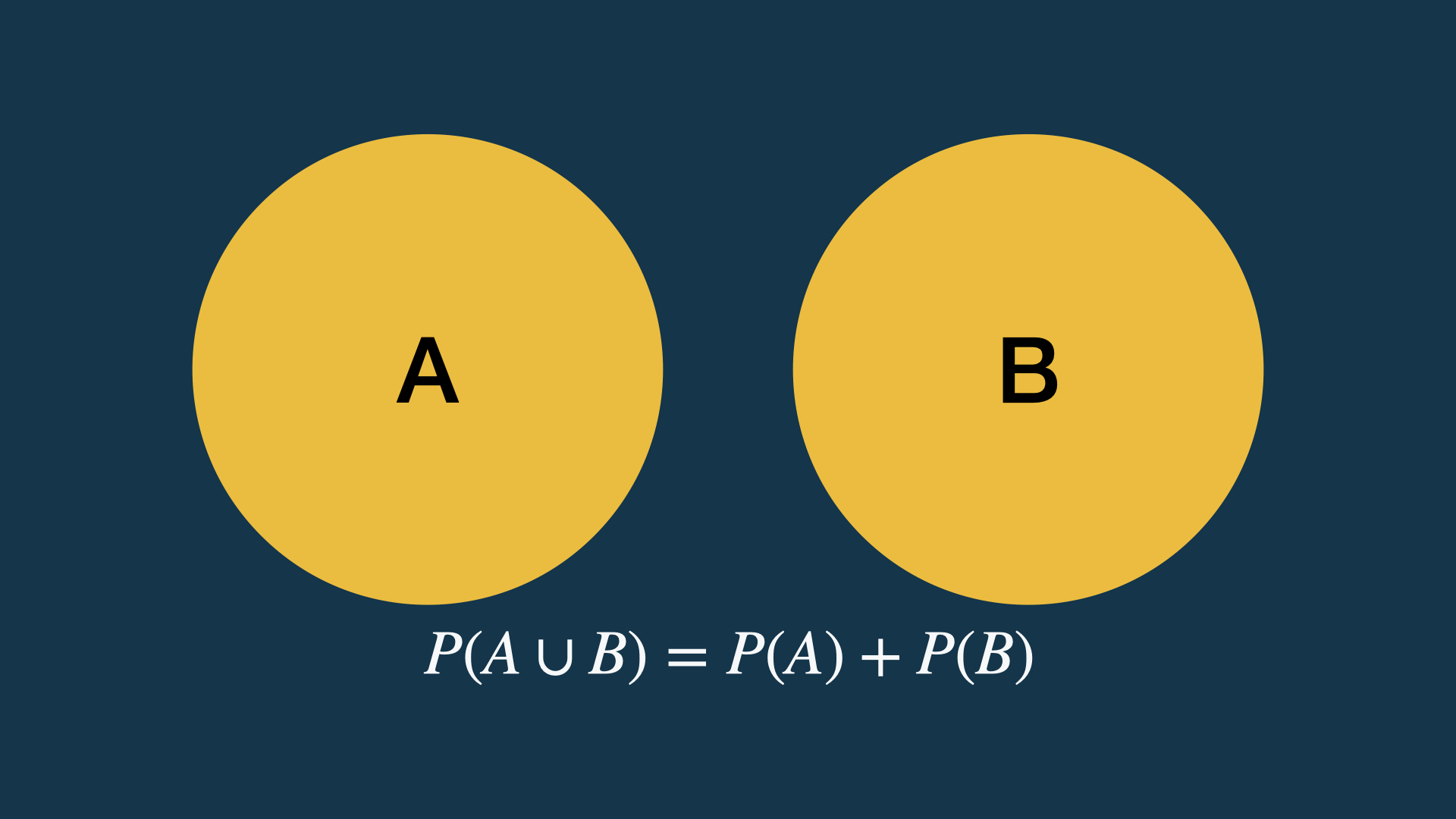
Laws of Probability: Addition (2)

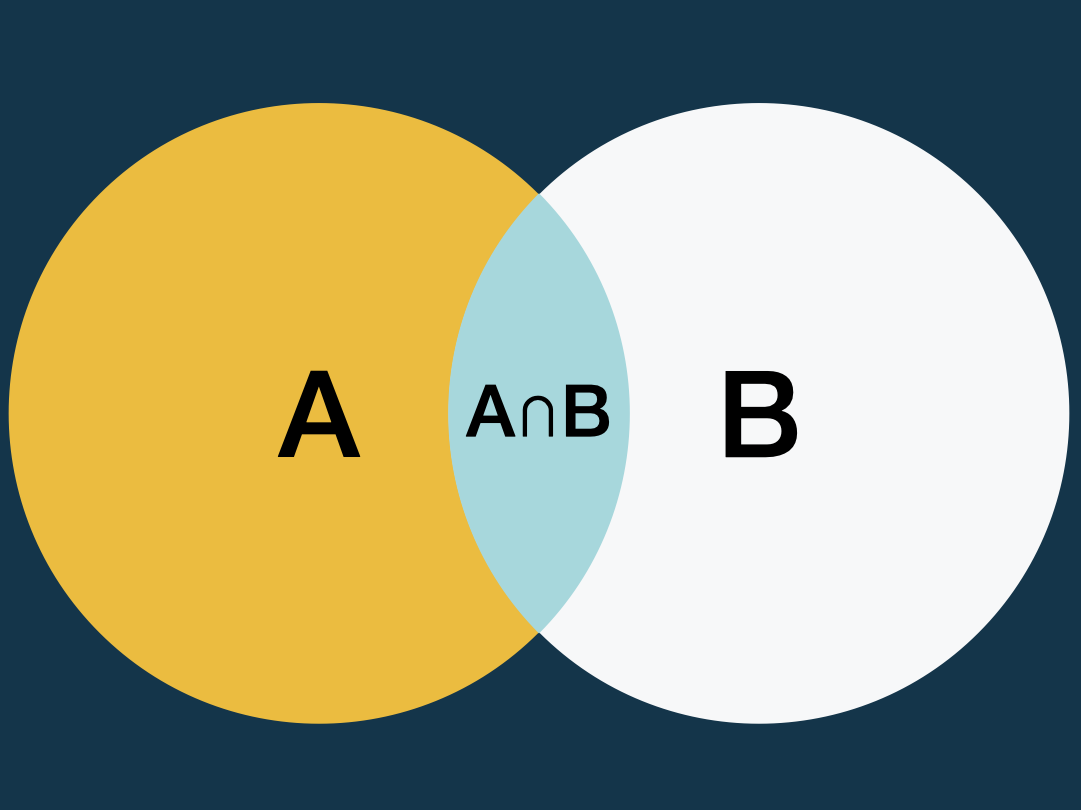
Addition (summation of probabilities) of non-exclusive events.

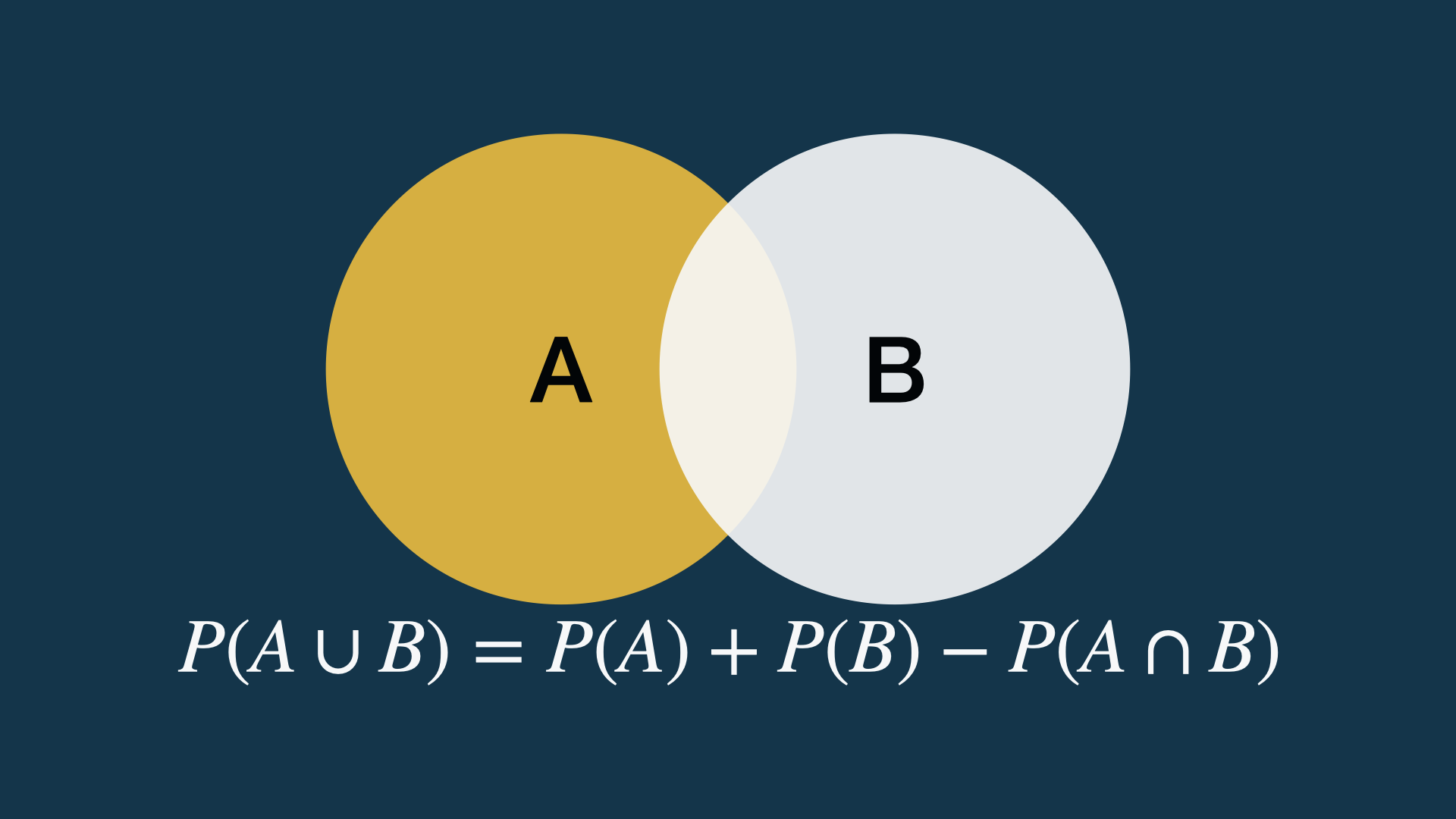
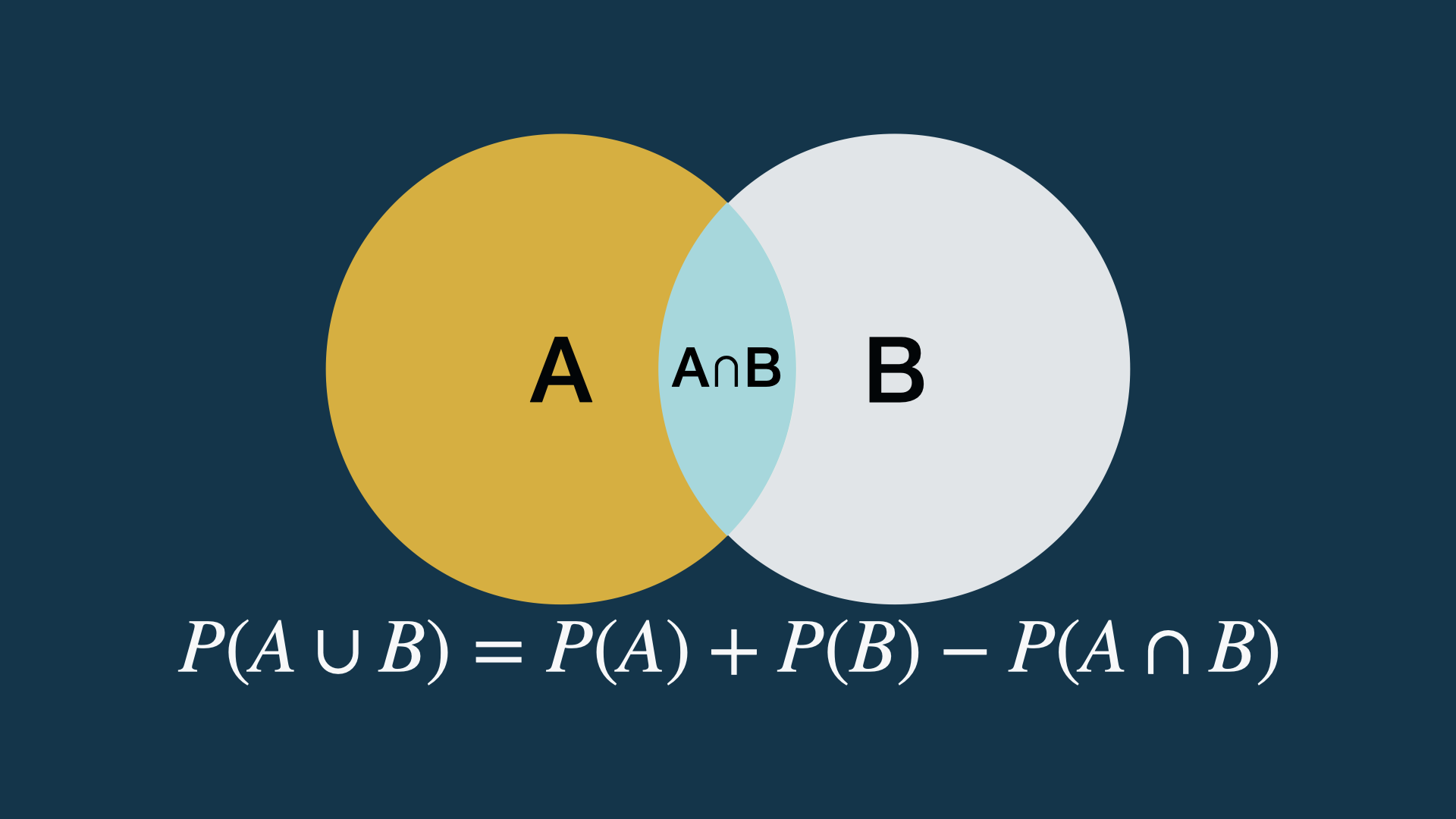
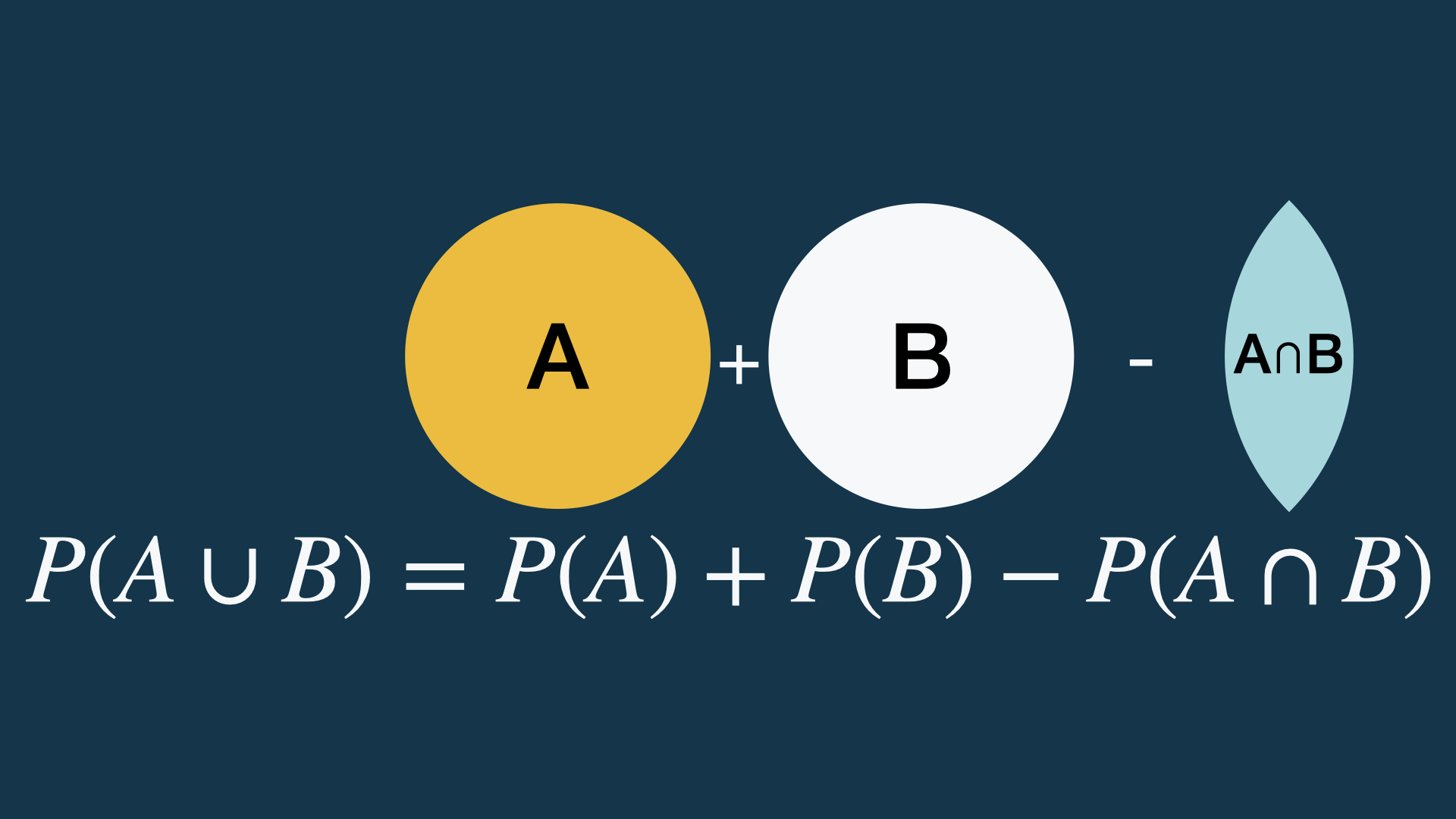
Laws of probability: multiplication

Multiplication of exclusive events.

\[ P(A \cap B) = P(A) \times P(B) \]

Conditional probability

\[ P(A \cap B) = P(A) \times P(B|A) = P(B) \times P(A|B) \]

Probability in diagnostics

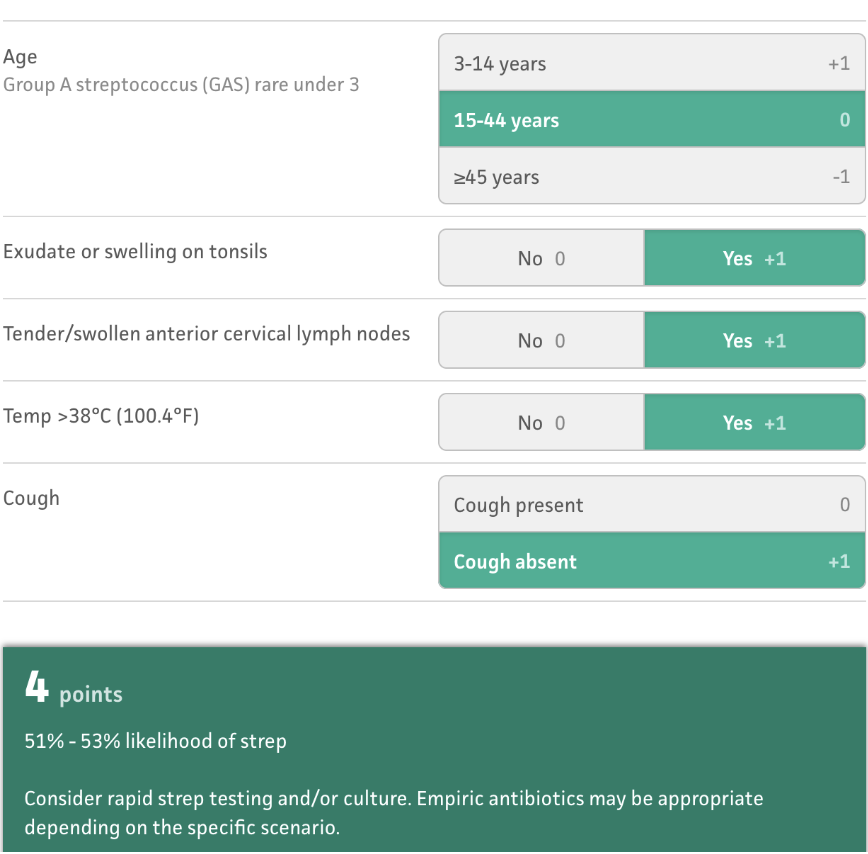
CENTOR Score

• The contribution of each symptom/sign to the likelihood of strep. infections
• The result is a pre-test probability

Theoretical probability distributions

Theoretical probability distributions are specific mathematical descriptions (models) of random phenomena.

• Binomial
• Normal

Mathematical model

Mathematical model

Reality

Bernoulli’s experiment

• A model of the coin tossing process.
• Basic building unit for other distributions.

A coin tossed once:

rbinom(n = 1, size = 1, prob = 0.5)

[1] 0

Coin tossed 10 times:

rbinom(10, 1, 0.5)

 [1] 1 1 0 0 1 0 1 1 0 0

Binomial distribution

Conditions:

• Exclusive events
• Constant probability
• Independent

The binomial probability is given by:

\[ P(X = x) = \frac{n!}{x!(n-x)!}p^{x}q^{n-x} \]

Exercise 1

The frequency of hypertension in the population over 65 years old is 42%.

What is the probability that two people with hypertension will be in a

random sample of 7 people chosen from that same population?

Why is the normal distribution frequent?

• The normal distribution is created by adding (or multiplying) the results of many smaller processes.
• Measurement errors, growth variations, and molecular velocity are examples of such processes.

Poređaj 1000 svojih najbližih prijatelja na sredinu fudbalskog terena. Svako ima novčić u ruci. Kad padne glava ide se korak napred, a kad padne pismo korak nazad. Nakon 16 bacanja izmeri udaljenost od pocetne linije. Da li možes da znas proporciju ljudi koja stoji na liniji? A 5 metara od linije? I ako ne znamo gde će pojedinačna osoba završiti, možemo znati koje će udaljenosti biti najčešće.

Normal distribution

Standard normal distribution

Normal distribution where \(\bar x = 0\) and \(sd = 1\). It is given by the formula:

\[ z_i = \frac{x_i - \mu}{\sigma} \]

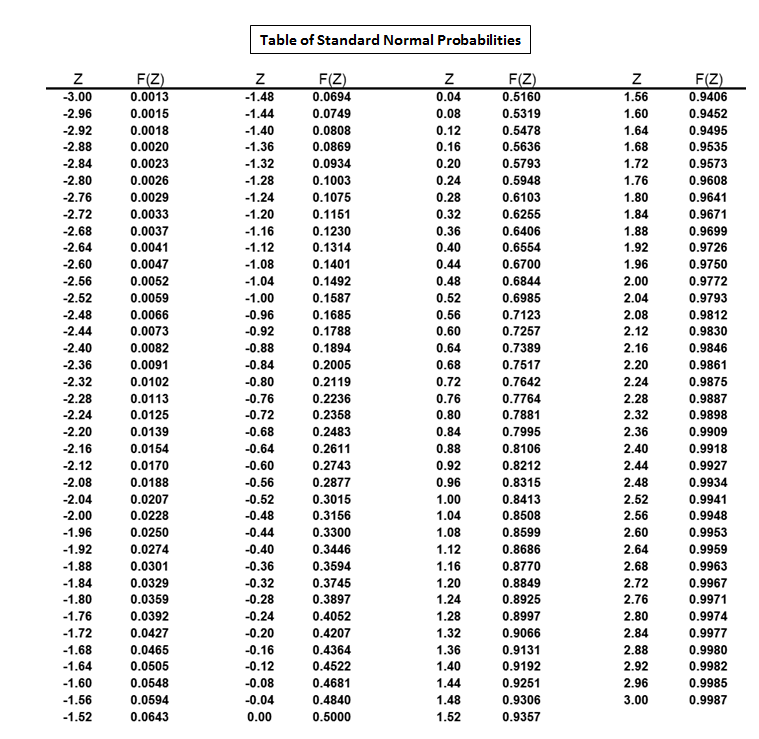
It used to be important when calculation was done by hand via probability tables.

Inace bi morali da napravimo beskonacno tablica verovatnoca; za svaku mogucu normalnu distribuciju.

Probability table

30 “zakljucanih” ljudskih kalkulatora koji racunaju verovatnocu.

Student’s t-distribution

100 god stara.Varijabilitet populacije nespoznat, pa cemo uzeti iz uzorka, sto dodaje jos nesigurnosti. Za svaki stepen slobode (koliko informacija smo iskoristili da procenimo variabilitet) postoji posebna t-distribucija. t-dist se priblizava z-dist za beskonacno stepena slobode.

Chi-square distribution

Uzorci iz Z-dist² (postaju pozitivni) i to postane hi-kvadrat. (sum of square deviations) / (pop. variance) -> kako idu df inf hi postaje z. F dist. (dist of ratio of two variances)

68-95-99.7%

Exercise 2

In a population of women between the ages of 25 and 50, serum uric acid values

are normally distributed with a mean 333 mmol/L and a

standard deviation 30 mmol/L.

What is the probability that a randomly selected person from this population has a

serum uric acid value greater than 410 mmol/l?

Probability calculation: normal distribution