Testiranje normalnosti i transformacije podataka

Dr Nikola Grubor

2024-11-26

Zašto transformišemo podatke?

• Parametarski testovi imaju veću moć od neparametarskih ako su uslovi normalnosti ispunjeni
• Uslov normalnosti često nije opravdan, a centralna granična teorema važi za velike baze podataka
• Transformacija može biti lako rešenje
• Neparametarske metode (Wilcoxon, Mann-Whitney U) su dobra alternativa

Logaritamska transformacija

Logaritamska funkcija:

\[ y = log(x) \]

\[ log_{10}(1000) = 3 \]

Inverzna funkcija je:

\[ exp(y) = x \]

gde je,

\[ exp(y) = 10^y \]

Primer transformacije

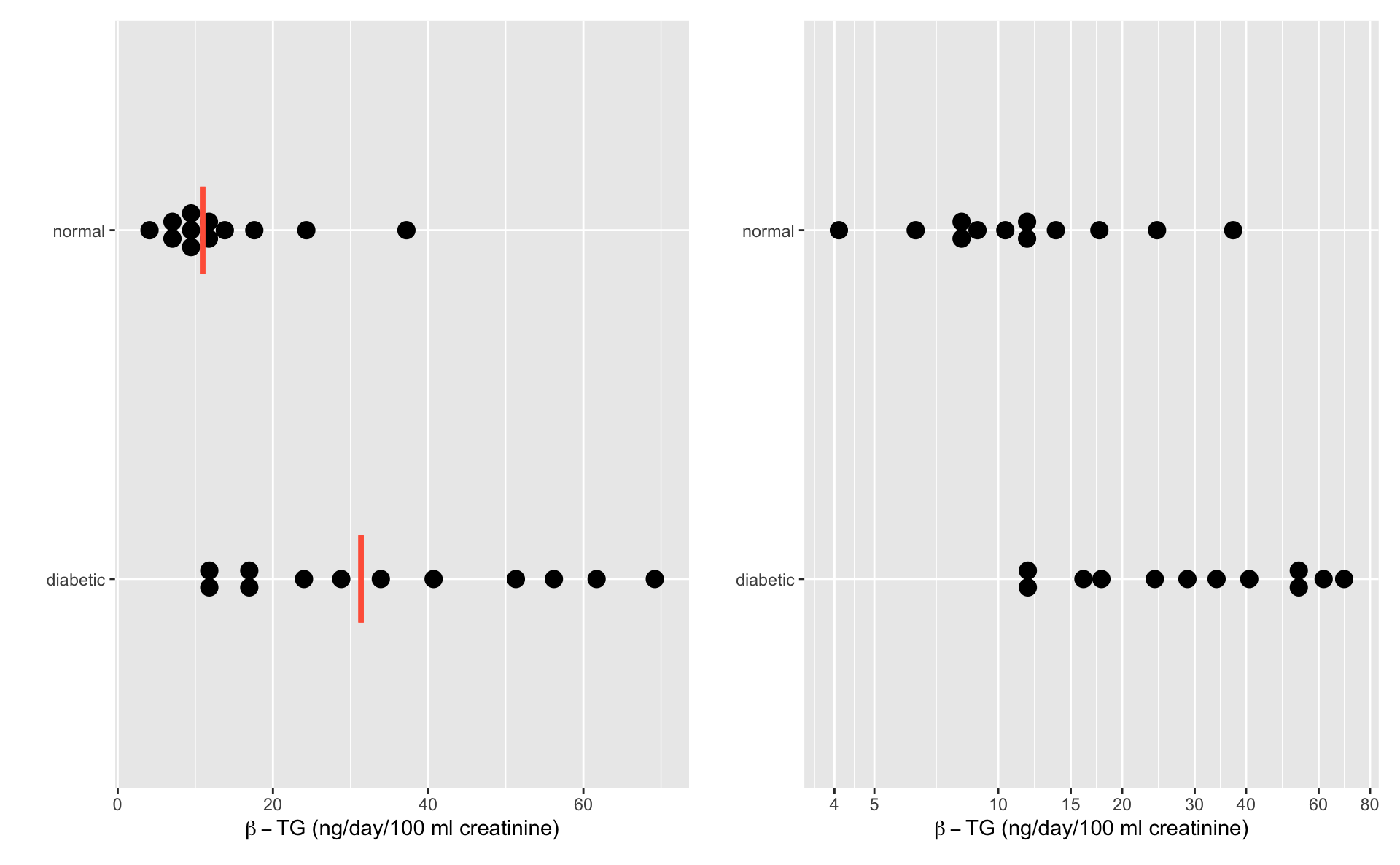
Upotreba testa na transformisanim podacima

t.test(btg ~ status, data=d)

    Welch Two Sample t-test

data:  btg by status
t = 3.3838, df = 15.343, p-value = 0.003982
alternative hypothesis: true difference in means between group diabetic and group normal is not equal to 0
95 percent confidence interval:
  8.07309 35.41024
sample estimates:
mean in group diabetic   mean in group normal 
              35.27500               13.53333 

t.test(log(btg) ~ status, data=d)

    Welch Two Sample t-test

data:  log(btg) by status
t = 3.8041, df = 21.9, p-value = 0.0009776
alternative hypothesis: true difference in means between group diabetic and group normal is not equal to 0
95 percent confidence interval:
 0.4352589 1.4792986
sample estimates:
mean in group diabetic   mean in group normal 
              3.390628               2.433349 

Neparametarski testovi kao alternativa

wilcox.test(btg ~ status, data=d)

    Wilcoxon rank sum test with continuity correction

data:  btg by status
W = 125.5, p-value = 0.002209
alternative hypothesis: true location shift is not equal to 0

wilcox.test(log(btg) ~ status, data=d)

    Wilcoxon rank sum test with continuity correction

data:  log(btg) by status
W = 125.5, p-value = 0.002209
alternative hypothesis: true location shift is not equal to 0

Bitno

Neparametarski testovi se ponašaju isto na log-transformisanim podacima.

Provera normalnosti

• Testiraju nultu hipotezu da su podaci poreklom iz normalne distribucije
• Shapiro-Wilk teoretski ima veću statistićku snagu of Kolmogorov-Smirnov testa

Shapiro-Wilk

shapiro.test(rnorm(1000, 5, 3))

    Shapiro-Wilk normality test

data:  rnorm(1000, 5, 3)
W = 0.99838, p-value = 0.4765

Kolmogorov-Smirnov

• Zahteva specifikaciju iz koje distribucije su dosli podaci
• EZR to radi sam tako što procenjuje aritmetički sredinu i standardnu devijaciju iz samih podataka

x <- rnorm(50)
y <- runif(30)
# Da li su x i y iz iste distribucije?
ks.test(x, y)

    Exact two-sample Kolmogorov-Smirnov test

data:  x and y
D = 0.44, p-value = 0.0009116
alternative hypothesis: two-sided

Performanse Shapiro-Wilkovog testa

• Na malim uzorcima ne odbacuje nultu dovoljno često
• Na velikim uzorcima odbacuje previše

x <- replicate(100, { # generise 100 testova na svakoj distribuciji
                     c(shapiro.test(rnorm(10)+c(1,0,2,0,1))$p.value,   #$
                       shapiro.test(rnorm(100)+c(1,0,2,0,1))$p.value,  #$
                       shapiro.test(rnorm(1000)+c(1,0,2,0,1))$p.value, #$
                       shapiro.test(rnorm(5000)+c(1,0,2,0,1))$p.value) #$
                    } # rnorm daje uzorak i normalne distribucije
               )
rownames(x) <- c("n10","n100","n1000","n5000")

Proporcija statistički značajnih testova:

  n10  n100 n1000 n5000 
 0.04  0.07  0.13  0.77 

QQ grafikoni normalnih distribucija

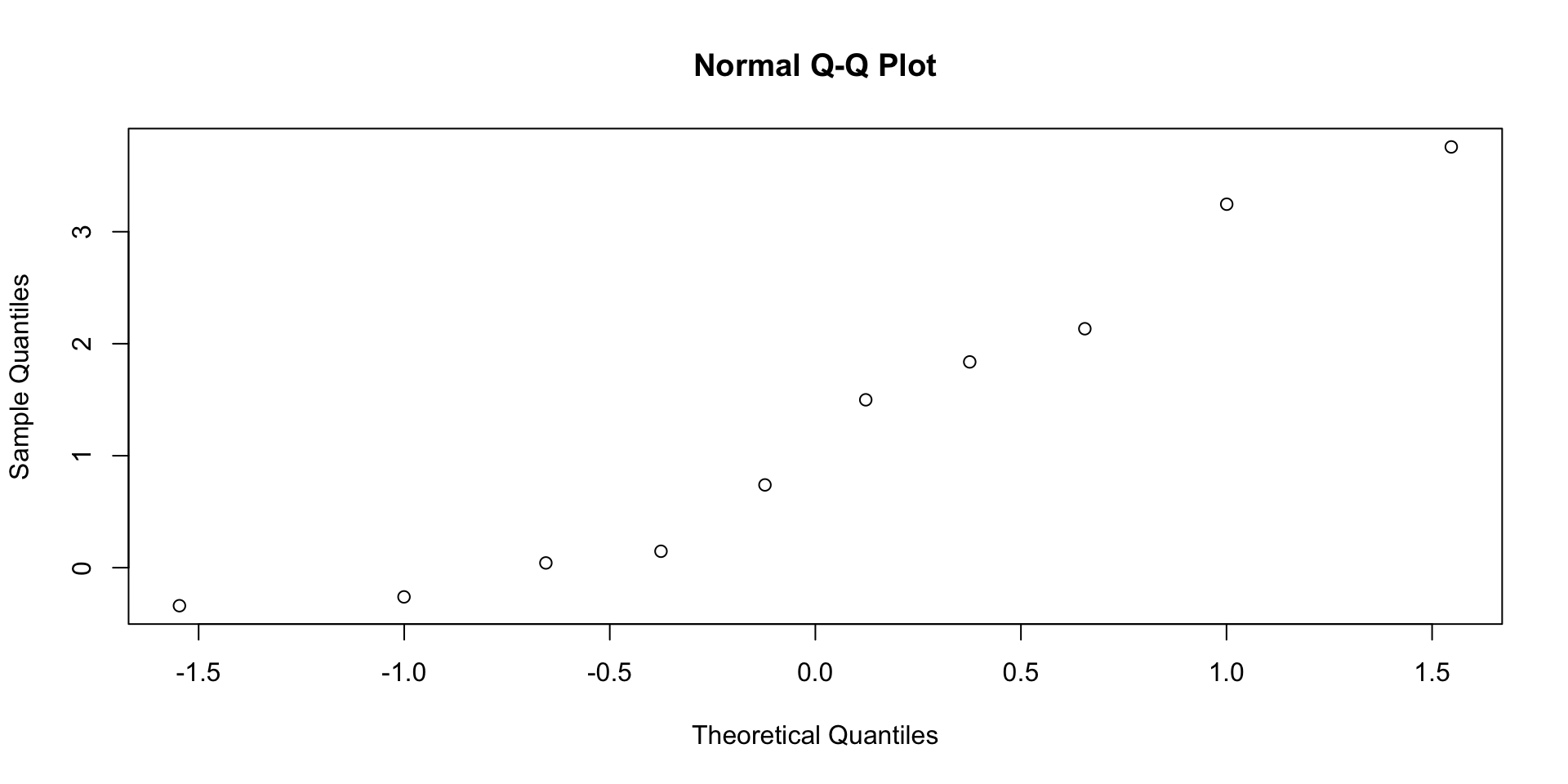
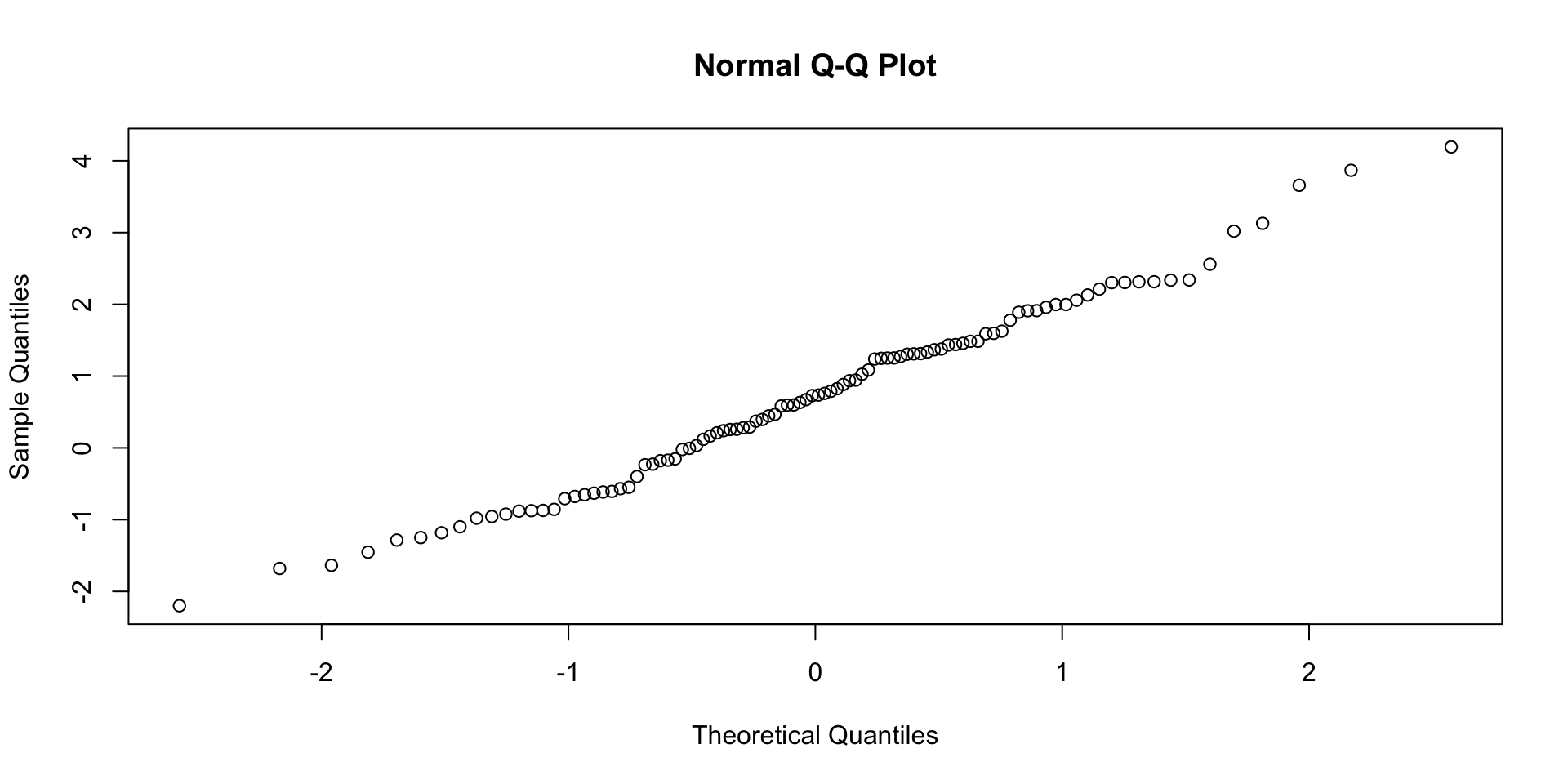
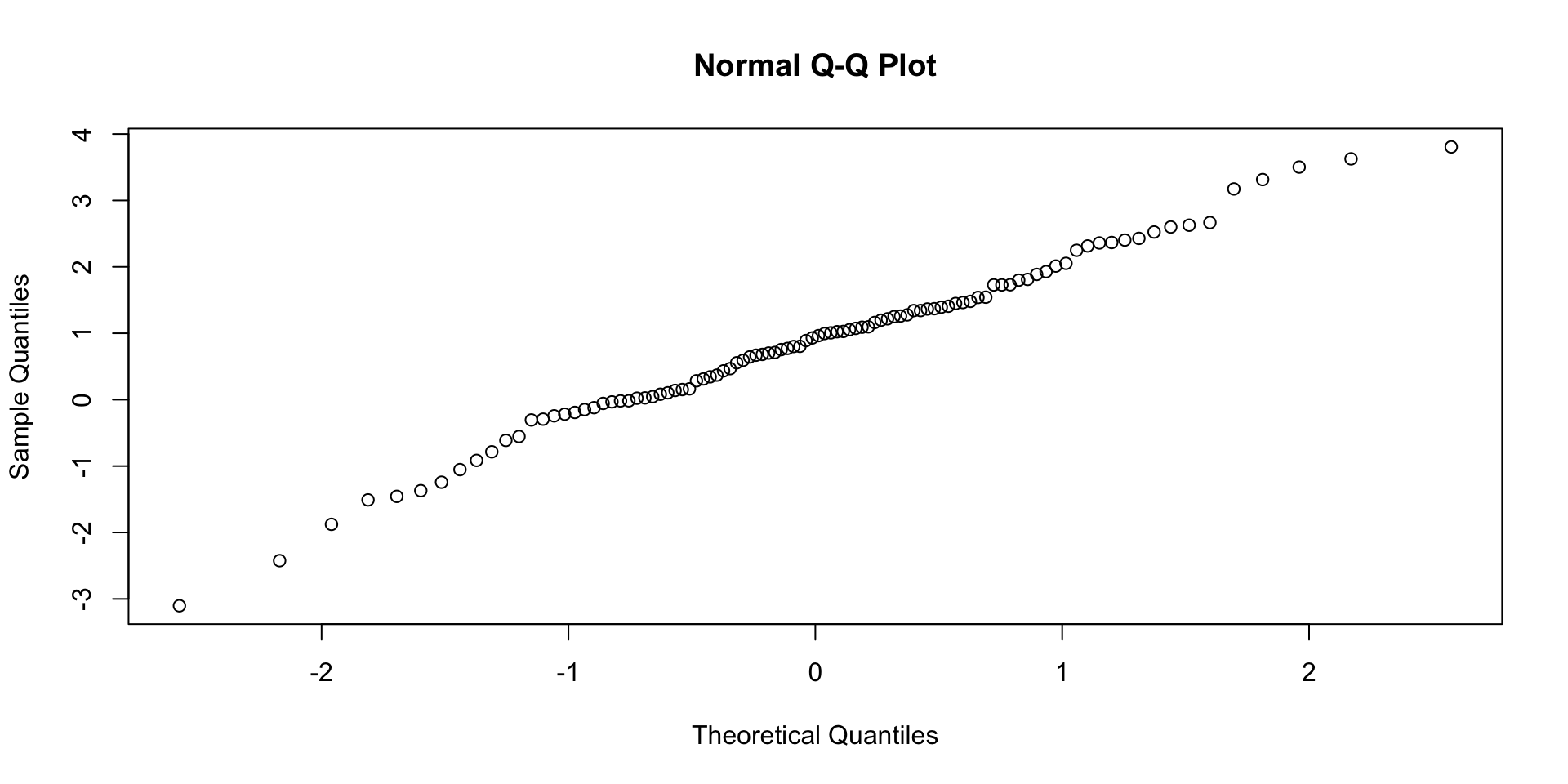
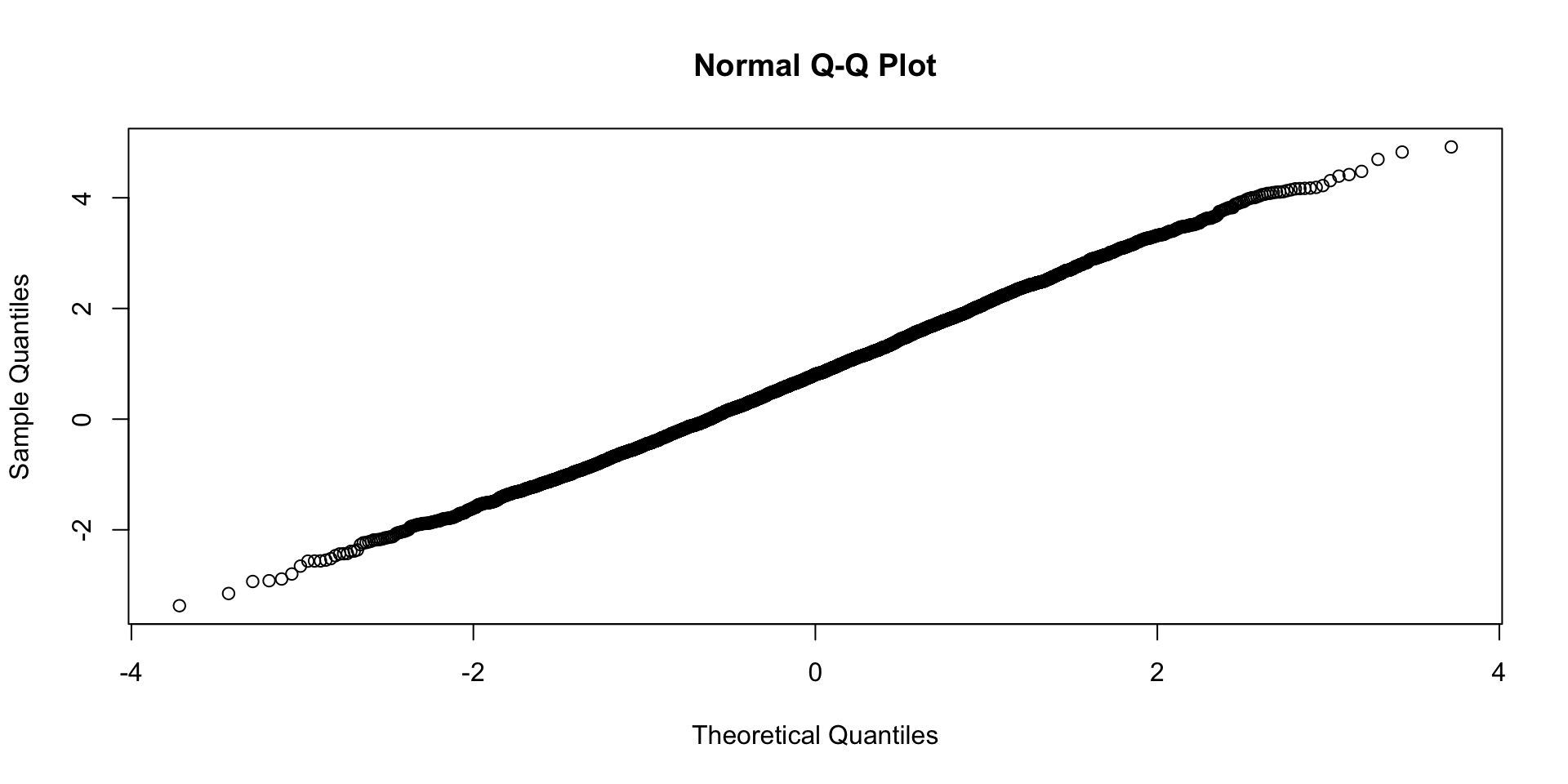
Upotreba testiranja normalnosti

Saveti

• Podaci se normalno raspodeljuju kada ima mnogo sitnih uticaja koji se sabiraju ili množe
• Neparametarski testovi se uvek mogu upotrebiti (poznato je da efikasnost 95% u odnosu na t-test kada su podaci normalni)
• Tesitrai normalnost je OK, ali ne doprinosi mnogo

Koje varijable prikupljati